Question

A rectangular field is of dimension $40\,m$ by $30\,m$. What distance is saved by walking diagonally across the field?

Answer 1

Hint: In this question we have a rectangular field whose length and breadth is given and it is asked what distance is saved by walking diagonally across the field. Firstly we will find the length of the diagonal by using Pythagoras theorem. Then we will take two points and calculate the distance between them through the diagonal and through the border. Finally we will subtract the value to get the desired answer.

Complete step by step answer:
A rectangular field is given to us such that its dimension is as follows:
Length $=40\,m$ and Breadth $=30\,m$.
As we know that each angle of a rectangle is of ${{90}^{\circ }}$ so let us make a rectangle with above dimension named as $ABCD$ as follows:

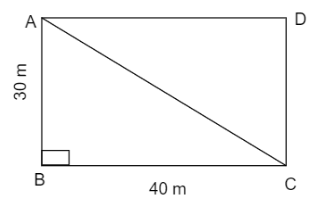
As we can see that $ABC$ is a right-angle triangle and $AC$ is our diagonal so we will use Pythagoras theorem to find the length of the diagonals follows:
Pythagoras Theorem for a right angle triangle $ABCD$ is as follows:
$A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}$
Substituting the value above from the diagram we get,
$A{{C}^{2}}=\left( 30\,{{m}^{2}} \right)+{{\left( 40\,m \right)}^{2}}$
$\Rightarrow A{{C}^{2}}=900\,{{m}^{2}}+1600\,{{m}^{2}}$
Taking square root on both sides we get,
$\Rightarrow AC=\sqrt{900\,{{m}^{2}}+1600\,{{m}^{2}}}$
$\Rightarrow AC=\sqrt{2500\,{{m}^{2}}}$

We know the number inside the square root is a perfect square of $50$ so we get,
$AC=50\,m$
Now if we walk from point \[A\] to $C$ through the diagonal the distance covered is
$AC=50\,m$……$\left( 1 \right)$
If we walk from point $A$ to $C$ through the point $B$ the distance covered is
$\Rightarrow 30\,m+40\,m$
$\Rightarrow 70\,m$…..$\left( 2 \right)$
So the distance saved is calculated by subtracting equation (1) and (2) as follows:
Distance Saved $=70\,m-50\,m$
Distance Saved $=20\,m$

So $20\,m$ distance is saved by walking diagonally in the field.

Note: A rectangular shape is the one having the opposite side the same and each angle inside the rectangle is of ${{90}^{\circ }}$. Pythagoras theorem is used to find the side of a right-angle triangle. It states that the square of the side opposite of the right angle known as Hypotenuse is equal to the sum of the square of the other two sides. This theorem is only true for a right-angle triangle.