Question

A rectangular field is 16 m long and 10 m wide. There is a path of uniform width all around it having an area of \[120\,{m^2}\]. Form the quadratic equation.

Answer 1

Hint: Here in this question, we have to find the quadratic equation. To solve this, given a length and width of rectangle field using that find length and width of a rectangle path which around a given rectangular field and later by the formula of area of rectangle i.e., \[\text{Area of rectangle = length} \times \text{breadth}\] on substituting the values and by further simplification we get the required solution.

Complete step by step solution:
Given the measurement of the rectangular field i.e., \[PQRS\] which is 16m long and 10 m wide.
Length of rectangle \[PQRS = PQ = 16\,m\]
Breadth of rectangle \[PQRS = QS = 10\,m\]

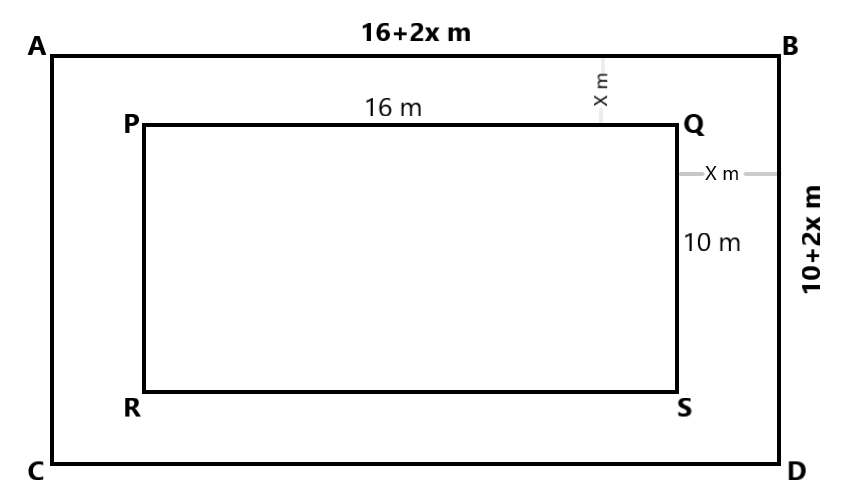
The path \[ABCD\] of uniform width around a rectangular field \[PQRS\] having an area of rectangular path is\[120\,{m^2}\].
Uniform width =\[x\,m\]
Length of rectangle \[ABCD = AB = 16 + 2x\]
Breadth of rectangle \[ABCD = AD = 10 + 2x\]
Area of rectangle \[ABCD\]= area of rectangular path + area of rectangle \[PQRS\]
Area of rectangle \[ABCD\]= \[120\,{m^2} + 16\,m \times 10\,m\]
 Area of rectangle \[ABCD\]= \[120\,{m^2} + 160\,{m^2}\]
Area of rectangle \[ABCD\]= \[280\,{m^2}\]
Now, by the formula of area of rectangle: \[Area = length \times breadth\].
\[ \Rightarrow \,\,Area{\text{ }}of{\text{ }}rectangle\,ABCD = AB \times AD\]
\[ \Rightarrow \,\,280\,{m^2} = \left( {16 + 2x} \right) \times \left( {10 + 2x} \right)\]
\[ \Rightarrow \,\,280\, = 16\left( {10 + 2x} \right) + 2x\left( {10 + 2x} \right)\]
\[ \Rightarrow \,\,280\, = 160 + 32x + 20x + 4{x^2}\]
\[ \Rightarrow \,\,280\, = 160 + 52x + 4{x^2}\]
Subtract both side by 280, then
\[ \Rightarrow \,\,0 = 160 + 52x + 4{x^2} - 280\]
\[ \Rightarrow \,\,0 = 4{x^2} + 52x - 120\]
Or
\[ \Rightarrow \,\,4{x^2} + 52x - 120 = 0\]
Take out 4 as common, then
\[ \Rightarrow \,\,4\left( {{x^2} + 13x - 30} \right) = 0\]
Divide both side by 4, then we get
\[ \Rightarrow \,\,{x^2} + 13x - 30 = 0\]
The above equation resembles the equation \[a{x^2} + bx + c = 0\].
Therefore, \[{x^2} + 13x - 30 = 0\] is a quadratic equation.

Note:
In the question they have mentioned the field in the rectangular shape so we consider the formula of area of rectangle. Suppose, if they mention any other plane figures we will consider the formula of respective plane figure. The quadratic equation is in the form of a polynomial equation whose degree is 2. Here, the unknown variables of the polynomial equation will represent the length and breadth of the rectangle.