Question

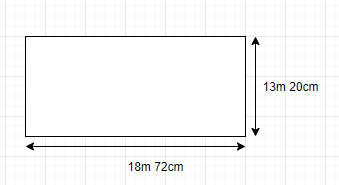
A rectangular courtyard is 18m 72cm long and 13m 20cm broad. It is to be paved with square tiles of the same size. Find the least possible number of such tiles?

Answer 1

Hint- Here we will proceed by calculating the area of the rectangular courtyard using the formula of rectangle=length$ \times $ breadth. Then by using the concept of HCF in the given length and breadth of the rectangular courtyard and using the formula of square i.e. $ = {\left( {side} \right)^2}$, we will get the area of the side of the tile. Hence we will find the number of tiles by dividing the area of the rectangular courtyard and the area of the side of tile.

Complete step-by-step answer:

HCF is the highest common factor which means the greatest number which can divide the given number. It is also known as the greatest common divisor(GCD).
We will first convert the unit of given length and breadth of the rectangular courtyard.
Length of rectangular courtyard = 18m 72cm = 1872cm.
Breadth of rectangular courtyard = 13m 20cm = 1320cm.
Using area of rectangle = $l \times b$
We get,
Area of rectangular courtyard = $1872 \times 1320$
Area of rectangular courtyard = 2471040cm.
Now we will find HCF of 1872 and 1320 in order to get area of side of tile and then we will use Euclid’s division Lemma –
1872 = 1320$ \times $ 1 + 552
Or 1320 = 552$ \times $2 + 216
Or 552 = 216$ \times $2 + 120
Or 216 = 120$ \times $1 + 96
Or 120 = 96$ \times $1 + 24
Or 96 = 24$ \times $4 + 0
HCF of 1872 and 1320 = 24
Also we are given that tile is square, so area of squared tile $ = {\left( {24} \right)^2}$= 576cm
By using the area of square $ = {\left( {side} \right)^2}$
Therefore, the area of the side of tiles is 576cm.
Here we will calculate the number of tiles by using the area of the rectangular courtyard and area of the side of tile which is now calculated.
Number of tiles = $\dfrac{{area{\text{ of rectangular courtyard}}}}{{area{\text{ of side}}\;{\text{of tile}}}}$
$ \Rightarrow $ $\dfrac{{1872 \times 1320}}{{24 \times 24}}$
$ \Rightarrow $4290
$\therefore $ 4290 tiles of the same size can be paved in the rectangular courtyard.
Note – In order to solve this type of question, we must concentrate on the conversion of units of length and breadth of rectangular courtyard. Also concept of Euclid’s division lemma i.e. if two positive integers a and b then there exists unique integers q and r such that which satisfies the condition a = b$ \times $ q + r where $0 < = r < = b$ is used in the question to get the required result.