Question

A rectangular card-board sheet has length 32 cm and breadth 26 cm. Squares each side 3 cm, are cut from the corners of the sheet and the sides are folded to make a rectangular container. Find the capacity of the container formed.
(A) $1560cu.cm$
(B) $1540cu.cm$
(C) $1550cu.cm$
(D) $1500cu.cm$

Answer 1

Hint: In this question, we need to evaluate the volume of the box formed on folding the sides of the rectangular sheet such that squares each of side 3 cm, are cut from the corners of the sheet. For this we will obtain the dimensions of the container by subtracting 6 from the card-board’s length and breadth each. Using the side of the square corner as height of the container, we get the capacity by taking the product of the dimensions of the container.

Complete step-by-step solution:
We are given the dimensions of a rectangular card-board sheet.
Its length is given as 32 cm and breadth as 26 cm.
Also, it is given that a rectangular container is created by cutting the corners of the sheet and folding the sides thus obtained.
The cut corners are squares of side 3cm each.
We are asked to calculate the capacity of the rectangular container.
That is, we need to find the volume of the rectangular container.

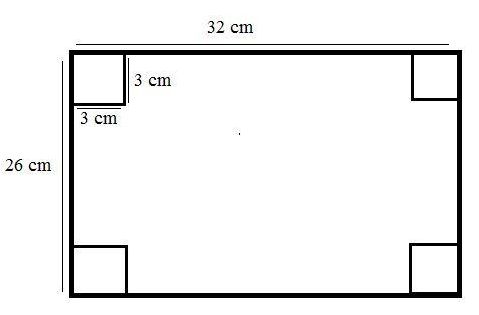
Now, originally, the length of the card-board was 32 cm and breadth was 26 cm.
But by cutting the corners, we can see in the figure that the new length will be $32 - 6 = 26cm$.
Similarly, the new breadth will be $26 - 6 = 20cm$
And the height will be the side of the square corners which is 3 cm.

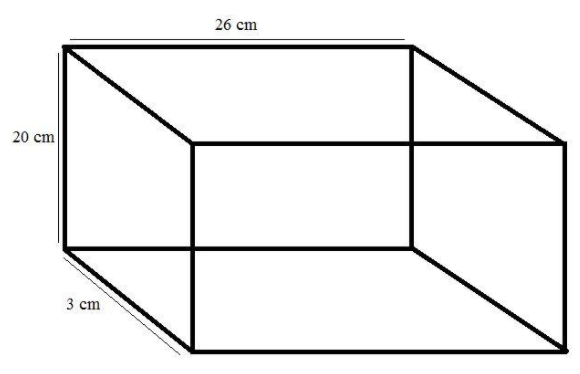
Let us denote the new length, breadth and height of the rectangular container by l, b, and h respectively.
Therefore, using these new dimensions, we get
Volume of the rectangular container$ = l \times b \times h = 26 \times 20 \times 3 = 1560cu.cm$.
Hence the capacity of the container formed is $1560cu.cm$.

Thus the correct answer is option ‘A’.

Note: It is interesting to note that when the sheet is folded to make the box then the height of the box will be same as the length of the side of the square that has been cut-out from the rectangular sheet and the length and width of the box will me equals to the length and the width of the rectangular sheet subtracted by the length of the square. Some students tend to subtract only 3 cm from the original length or breadth to obtain the new dimensions. This is a mistake which will lead you to a wrong answer.