Question

A rectangular A4 size paper is kept on cartesian plane coinciding the points
(1, 1), (−1, 0), (0,−2). Find the perimeter of the paper.
A. 12
B. 8$\sqrt 5 $
C. 4$\sqrt 5 $
D. 10

Answer 1

Hint: In order to solve this problem we need to use the distance formula as the coordinates are given. We can simply use distance formulas to find the sides of the rectangle. Then we just need to apply the formula of the perimeter of the rectangle and get the right answer.

Complete step-by-step answer:
We know that the distance between the point $({x_1},{y_1})$ and $({x_2},{y_2})$ is $\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $.
To get this problem solved we will draw a rough figure and calculate the lengths of adjacent sides then we can calculate the perimeter of the rectangle.

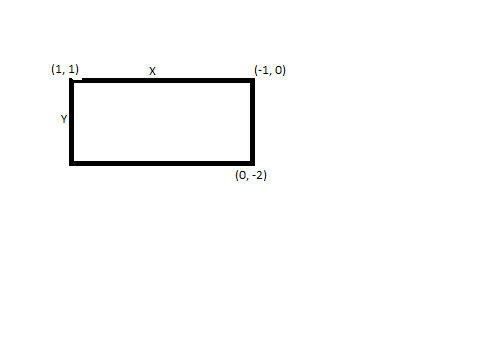
We need to calculate X and Y with the help of distance formula and then the perimeter will be 2(X+Y).
We have the points (1, 1) and (-1, 0).
So, the distance between these two points is,
X = $\sqrt {(1 - {{( - 1)}^2} + {{(1 - 0)}^2}} = \sqrt 5 $.
The other two points are (-1, 0) and (0, -2).
Y =$\sqrt {{{( - 1 - (0))}^2} + {{(0 - ( - 2))}^2}} = \sqrt 5 $
Y=$\sqrt 5 $
Now the perimeter will be 2(X+Y) = 2($\sqrt 5 $+$\sqrt 5 $).
Hence, the perimeter will be 4$\sqrt 5 $.

Note: When you get to solve such problems you need to know that in a rectangle only three coordinates are sufficient to get the value of all the terms like area and perimeter since opposite sides are equal in rectangle and every angle is 90 degrees. So, with the help of distance formula we found different lengths using the three coordinates only. Knowing this will solve your problem and will give you the right answers.