Question

A rectangle is randomly selected from the grid of equally spaced squares as shown in figure:

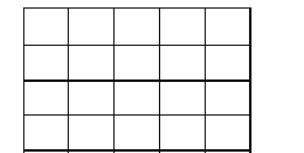
Find the probability that the rectangle is a square.

Answer 1

Hint: Here in the given question we need to find the probability for a random selection of a box, out of the drawn box, here we know probability means the ratio of favorable outcome to the total outcome, and accordingly we need to select the favorable and total outcome.

Complete step by step answer:
Here we need to select favorable box, out of the total box in the figure, here we need to first draw the table and mentioned the detail so to count the favorable and total possibilities:

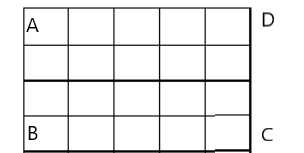
Here we can see there are five points along AB and six points along BC. In order to make a rectangle we choose two points from either side, so number of rectangle:
\[
  { \Rightarrow ^5}{C_2}{ \times ^6}{C_2} = \dfrac{{5!}}{{(5! - 2!)2!}} \times \dfrac{{6!}}{{(6! - 2!)2!}} = \dfrac{{5 \times 4 \times 3!}}{{3! \times 2!}} \times \dfrac{{6 \times 5 \times 4!}}{{4! \times 2!}} \\
  { \Rightarrow ^5}{C_2}{ \times ^6}{C_2} = \dfrac{{20}}{2} \times \dfrac{{30}}{2} = 10 \times 15 = 150 \\
 \]
Now we need to count the squares:
Here we need to count for one into one, then two into two, three into three and four into four square, since more than this no square is possible, now here we will select the points possible from AB and BC and then write accordingly, on solving we get:
Number of \[1 \times 1\] squares=\[4 \times 5 = 20\]
Number of \[2 \times 2\] squares=\[3 \times 4 = 12\]
Number of \[3 \times 3\] squares=\[2 \times 3 = 6\]
Number of \[4 \times 4\] squares=\[1 \times 2 = 2\]
Total number of squares= \[20 + 12 + 6 + 2 = 40\]
Required probability:
\[ \Rightarrow \dfrac{{40}}{{150}} = \dfrac{4}{{15}}\]
Here we get the required probability.

Note: Here the given question is from probability in which we need to use combination, property since combination, directly gives the total possibilities, which can occur from a given condition, here accordingly we use the property for rectangle, and then for square we need to count the total possibilities, thus solved accordingly.