Question

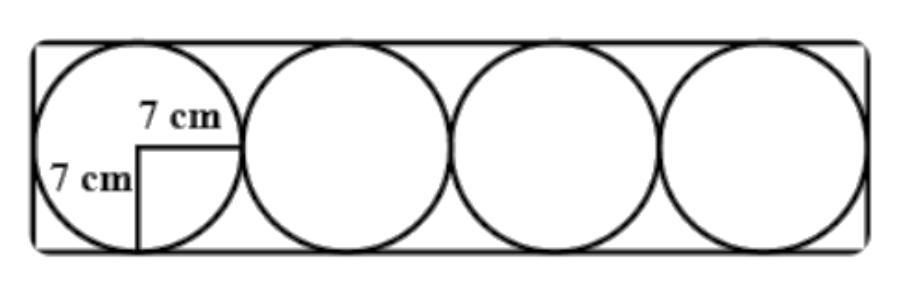
A rectangle encloses for circles. The radius of each circle is $7\,{\rm{cm}}{\rm{.}}$ Calculate the area of (a) the rectangle (b) the shaded portion.

Answer 1

Hint: Use the formula $A = l \times b$, where $l$ is the length and $b$is the breadth of the rectangle. Again use, $A = \pi \times {r^2}$, where $r$ is the radius. Finally, subtract the area of the circles from the area of the rectangle.

Complete step by step answer:
A solid object's surface area is a measure of the total space filled by the object's surface. In a rectangle, there are two types of dimensions required to fully explain a rectangle. It consists of length and breadth, where length is the longer side and the breadth is the shorter side.
Here, in this problem, the dimensions i.e. the length and breadth are directly not provided in the question. To find the length and breadth let’s reproduce the figure given in the question as follows:

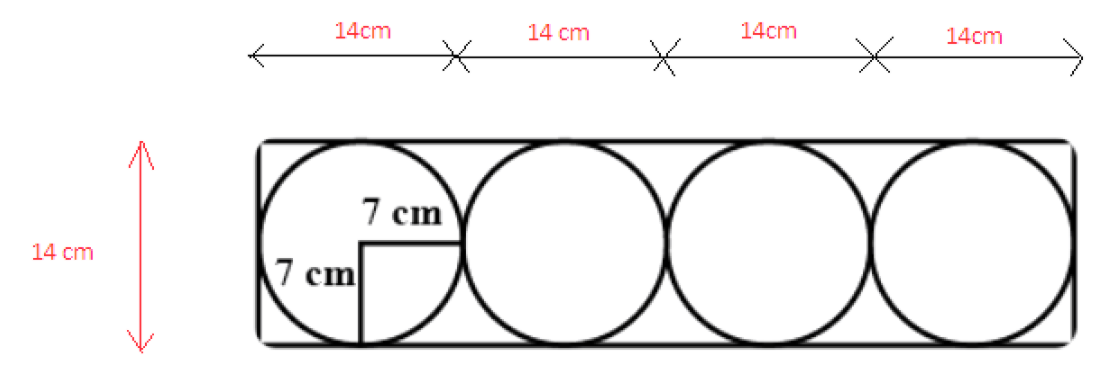
Since the rectangle encloses four circles, the length $\left( l \right)$ of the rectangle is the sum of the diameters of the four circles. The breadth $\left( b \right)$ of the rectangle is the diameter of one circle.
Hence,
$\begin{array}{c}l = \left( {14 + 14 + 14 + 14} \right)\,{\rm{cm}}\\{\rm{ = 56}}\,{\rm{cm}}\end{array}$
$\begin{array}{c}b = \left( {7 + 7} \right)\,{\rm{cm}}\\{\rm{ = 14}}\,{\rm{cm}}\end{array}$
The area of a rectangle is given by the formula:
$\begin{array}{c}A = l \times b\\ = 56\,{\rm{cm}} \times 14\,{\rm{cm}}\\{\rm{ = 784}}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\end{array}$
Hence, the area of the rectangle is found out to be ${\rm{784}}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}.$

Let us take the shaded portion be the area inside the rectangle, but excluding the circles.
To find out this area, we need to first calculate the area of all the four circles and then subtract this area from the area of the rectangle.
Radius $\left( r \right)$ of the circle in the given figure is ${\rm{7}}\,{\rm{cm}}.$
Area of a circle is given by a formula $A = \pi \times {r^2}$
Substituting the value of radius in the equation:
Area of one circle:
$\begin{array}{c}A = \pi \times {r^2}\\ = \dfrac{{22}}{7} \times {7^2}\\{\rm{ = }}\dfrac{{22}}{7} \times 7 \times 7\\ = 22 \times 7\\ = 154\,{\rm{c}}{{\rm{m}}^2}\end{array}$
Since, there are four circles so the total area of all the four circles is:
$\begin{array}{c}Area = 4 \times 154\,{\rm{c}}{{\rm{m}}^2}\\ = 616\,{\rm{c}}{{\rm{m}}^2}\end{array}$
Hence, the area of the shaded portion is:
$\begin{array}{l}{\rm{784}}\,{\rm{c}}{{\rm{m}}^{\rm{2}}} - 616\,{\rm{c}}{{\rm{m}}^2}\\ = 168\,{\rm{c}}{{\rm{m}}^2}\end{array}$

Note: In this given problem, you are asked to find the area of the rectangle and the area of the shaded portion. To find the length of the rectangle, count the number of circles inside it and add the diameter of all the circles. Since, there is no specific formula to find out the area of the shaded portion, so subtract the area of the circles from the area of the rectangle.