Question

A rectangle and a rhombus are on the same base and between the same parallels. Then the ratio of their areas is
(a) 1: 1
(b) 1: 2
(c) 1: 3
(d) 1: 4

Answer 1

Hint: In this question, draw the diagram with the conditions mentioned, use the side angle side (S-A-S) theorem to prove the required. Use the properties of rectangle and rhombus to prove the theorem and use other operations to reach the result.

Complete step-by-step answer:
Here we have a rhombus and a rectangle with the same base and lying between two parallel lines. So, let us find the ratio of their areas.
Let us draw the figure according to the conditions in the question,
 

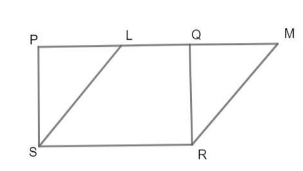
Let us consider, PQRS as a rectangle and LMRS as rhombus and SR being the common base as mentioned in the question.
No, let us take $ \vartriangle \text{PLS} $ and $ \vartriangle \text{QMR} $ ,
 $ \angle LPS=\angle MQR $ (both the angles are 90 degree)
side PS = side QR (both are the opposite sides of the rectangle)
side LS = side MR (both are the sides of the rhombus)
 $ \vartriangle \text{PLS}\cong \vartriangle \text{QMR} $ (By right angle side hypotenuse side congruence)
Therefore, area of triangle PLS = area of triangle QMR
Now, add the area of polygon LQRS on both sides of equation (i), we get
area of triangle PLS + area of polygon LQRS = area of triangle QMR + area of polygon LQRS
which automatically gives,
area of $ \square \text{PQRS}\,\text{=} $ area of $ \text{ }\square \text{LMRS} $
Solve the following further by dividing area (LMRS) on both sides
Now, we have
\[\dfrac{area\left( PQRS \right)}{area\left( LMRS \right)}=\dfrac{1}{1}\]
Hence, the ratio of there is 1:1.

Note: Here, the most important is drawing the figure with the necessary conditions or else it would be difficult to prove the theorem. Also, all polygons with four sides are known as Quadrilaterals. Note that adding or subtracting the same quantity on both sides of the equality will not affect the equality.