Question

A ramp for unloading a moving truck has an angle of elevation of ${{30}^{\circ }}$ . If the top of the ramp is 0.9m above the ground level, then find the length of the ramp.

Answer 1

Hint: Draw a figure as per the given details in the question and apply trigonometric formulas. Trigonometric formulas to be used:
$\begin{align}
  & \sin \theta =\dfrac{\text{Perpendicular}}{\text{hypotenuse}} \\
 & \cos \theta =\dfrac{\text{Base}}{\text{hypotenuse}} \\
 & \tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}} \\
\end{align}$
Complete step-by-step answer:
The angle of elevation is the angle between the horizontal line of sight up to and the line sight up to an object. For example if you are standing on the ground looking up at the top of a mountain you could measure the angle of elevation.

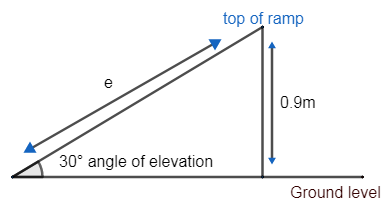
Let the length of ramp = l m
According to the formula of $\sin \theta $ -
$\sin \theta =\dfrac{\text{Perpendicular}}{\text{hypotenuse}}$ .
For a right triangle –

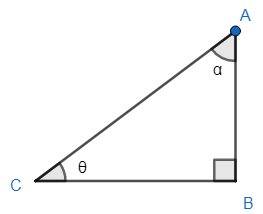
For $\theta -$ BC= Base
AB= perpendicular
AC= Hypotenuse
For $\alpha $ - AB= Base
BC = Perpendicular
AC= hypotenuse
Here:
For angle C, putting the value of its perpendicular and base in the formula for sin C, we will get-
$\begin{align}
  & \sin {{30}^{\circ }}=\dfrac{\text{Perpendicular}}{\text{hypotenuse}}=\dfrac{0.9}{l} \\
 & \Rightarrow \dfrac{1}{2}=\dfrac{0.9}{l} \\
\end{align}$
Multiply both sides of equation by 2, we will get
$\begin{align}
  & \Rightarrow l=2\times 0.9 \\
 & \Rightarrow l=1.8m \\
\end{align}$
Hence, the required length of ramp $1.8m$.

Note: Another method –

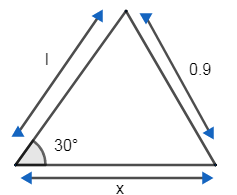
We know $\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}}$ .
So, $\tan {{30}^{\circ }}=\dfrac{0.9}{x}$
We know $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$
So, $\dfrac{1}{\sqrt{3}}=\dfrac{0.9}{x}$
$\Rightarrow x=0.9\sqrt{3}$
Next, we know –
${{\left( \text{hypotenuse} \right)}^{2}}={{\left( \text{perpendicular} \right)}^{2}}+{{\left( \text{base} \right)}^{2}}$
In this triangle –
$\begin{align}
  & \Rightarrow {{\left( \text{l} \right)}^{2}}={{\left( \text{0}\text{.9} \right)}^{2}}+{{\left( \text{x} \right)}^{2}} \\
 & \Rightarrow {{l}^{2}}=0.81+\left( 0.9\sqrt{3} \right) \\
 & \Rightarrow {{l}^{2}}=0.81+2.43 \\
 & \Rightarrow {{l}^{2}}=3.24 \\
\end{align}$ (above calculated $x=0.9\sqrt{3}$ )
Taking positive square root both sides –
$\begin{align}
  & \Rightarrow l=\sqrt{3.24} \\
 & \Rightarrow l=1.8m \\
\end{align}$