Question

A railway train is travelling on a circular curve of 1500 metres radius at the rate of 66km/h. Through what angle has the train turned in 10 seconds?

Answer 1

Hint: Find the length of the arc covered in by the train in 10 seconds. Hence find the angle turned by the train in 10 seconds.

Complete step-by-step answer:

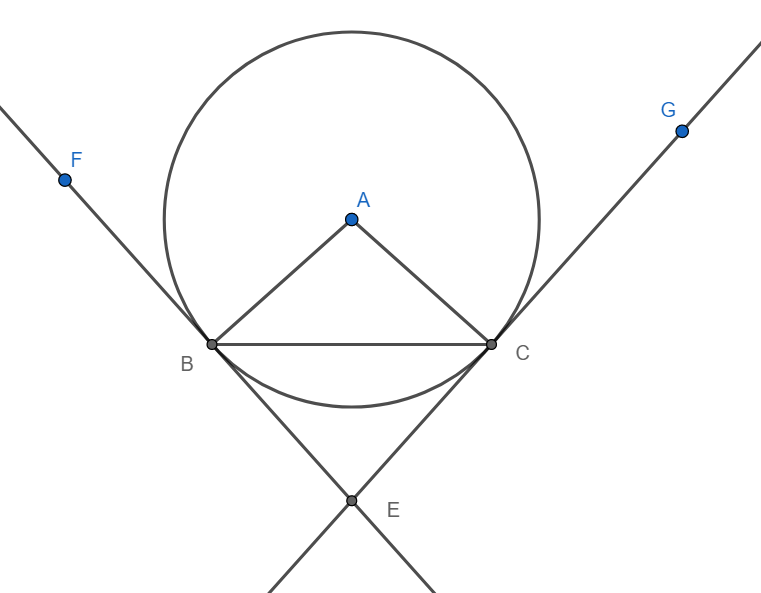
Let arc(BC) be the arc travelled by train in 10 seconds. Initially, the train is moving in BE direction. Finally, the train is moving in EC direction.
Hence the angle through which the train has turned is equal to $\pi -\angle BEC$.
Also, since ABEC is a cyclic quadrilateral, we have $\angle BAC+\angle BEC=\pi \Rightarrow \angle BAC=\pi -\angle BEC$
Hence, we have
$\angle BAC$ is the angle through which the train has turned.
Now, we have
Speed of the train $=66kmph=\dfrac{66\times 1000}{3600}m{{s}^{-1}}=\dfrac{55}{3}m{{s}^{-1}}$
Hence the train covers $\dfrac{55}{3}m$ in 1sec
Hence the distance covered by the train in 10 seconds $=\dfrac{55}{3}\times 10=\dfrac{550}{3}$
We know if x(in degrees) is the measure of an angle, l the length of the arc and r the radius of the circle, then $l=\dfrac{x}{360}\times 2\pi r$
Here $l=\dfrac{550}{3}m$ and $r=1500m$
Hence, we have
$\dfrac{550}{3}=\dfrac{x}{360}\times 2\pi \left( 1500 \right)$
Simplifying, we get
$x=\dfrac{550}{3}\times 360\times \dfrac{7}{3000\times 22}=7{}^\circ $
Hence the angle through which the train has turned in 10 seconds is $7{}^\circ $

Note: Alternative solution:
We know that $v=r\omega $ where v is the velocity of the train, r the radius of the circular track and $\omega $ is the angular velocity in radians/sec
Here $v=\dfrac{55}{3}$ and r = 1500
Hence, we have
$\dfrac{55}{3}=1500\omega $
Solving, we get
$\omega =\dfrac{11}{900}$ radians/sec
Converting radians/ sec into degrees/ sec, we get
$\omega =\dfrac{11}{900}\times \dfrac{180}{\pi }=\dfrac{11}{900}\times \dfrac{180}{22}\times 7=\dfrac{7}{10}$ deg/sec
We know that the angle covered in time t is given by $\theta =\omega t$
Hence the angle covered in 10 seconds $=\dfrac{7}{10}\times 10=7{}^\circ $