Question

A radio transmission tower is 210 feet tall. How long should a guy wire be if it is to be attached 11 feet from the top and is to make an angle of \[{{26}^{\circ }}\] with the ground?

Answer 1

Hint: To solve the given problem, we will first make a rough figure for it. The figure will make it easier to visualize the situation in the given problem. We should also know that in a right-angled triangle the sine function of an angle equals \[\dfrac{opposite}{hypotenuse}\]. Here, the opposite means the length of the opposite side to the angle.

Complete step by step solution:
We can make a rough figure for the situation in the given problem as follows,

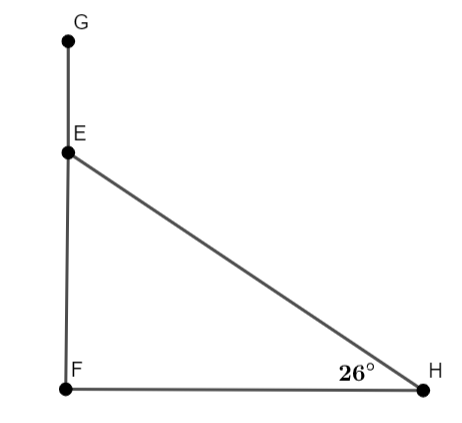
In above figure the length of \[GE\And GF\] equals 210 m and 11 m respectively. From above figure the opposite side to the angle of measure \[{{26}^{\circ }}\] has a length of \[210m-11m=199m\].
We know that in a right-angled triangle the sine function of an angle equals \[\dfrac{opposite}{hypotenuse}\]. Here, the opposite means the length of the opposite side to the angle. Here the hypotenuse side is \[EH\]which equals the length of the wire required.
Using this we can write the following equation \[\dfrac{EF}{EH}=\sin {{26}^{\circ }}\]. We can calculate the value of \[\sin {{26}^{\circ }}\] using calculator, substituting this value and the length of the opposite side in the above equation we get
\[\Rightarrow \dfrac{199}{EH}\approx 0.438\]
Solving the above equation, we get the length of the hypotenuse that is the length of wire required as \[453.95m\]. Thus this much wire is required.

Note: To solve these types problems, we should draw a rough figure for the given situation. As the figure will help in visualizing the situation. Generally, the angle given in such a problem is a standard angle whose trigonometric ratio values are already known, and we don’t need to calculate it using a calculator. Calculation mistakes should be avoided.