Question

A racing car moving towards a cliff sounds its horn. The driver observes that the sound reflected from the cliff has a pitch one octave higher than the actual sound of the horn. If $\upsilon $ is the velocity of sound then the velocity of the car is
\[\begin{align}
  & A)\dfrac{\upsilon }{\sqrt{2}} \\
 & B)\dfrac{\upsilon }{2} \\
 & C)\dfrac{\upsilon }{3} \\
 & D)\dfrac{\upsilon }{4} \\
\end{align}\]

Answer 1

Hint: We will be using the concept of Doppler Effect which states that there will be a variation in frequency if the source and observer are in relative motion. Here the variation is given as one octave higher which means the frequency will be doubled. We will find the velocity of the car by substituting this as the apparent frequency in the formula.

Formula Used:
$f'=f\left( \dfrac{\upsilon +{{v}_{o}}}{\upsilon -{{v}_{s}}} \right)$

Complete step by step answer:
Firstly we will try to draw a diagram for understanding the situation better.

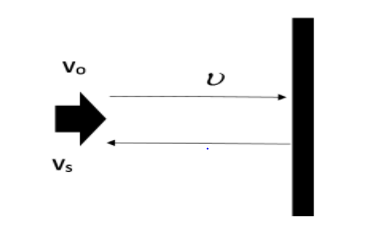
Here, $\upsilon $ is the velocity of sound, ${{v}_{o}}$and ${{v}_{s}}$ are the velocity of observer and source respectively. But we must be aware that the driver is sitting inside the car. So velocity of source and observer will be the same. Let us take thus velocity as $u$. i.e. ${{v}_{o}}={{v}_{s}}=u$
Let us take the initial frequency of the sound as $f$and final frequency as $f'$which is one octave higher than the initial frequency. i.e. $f'=2f$.
Then, the velocity of the car can be found using the Doppler Effect formula as,
 $\begin{align}
  & f'=f\left( \dfrac{\upsilon +{{v}_{o}}}{\upsilon -{{v}_{s}}} \right) \\
 & \Rightarrow 2f=f\left( \dfrac{\upsilon +u}{\upsilon -u} \right) \\
 & \Rightarrow 2\left( \upsilon -u \right)=\left( \upsilon +u \right) \\
 & \Rightarrow 2\upsilon -2u=\upsilon +u \\
 & \Rightarrow \upsilon =3u \\
 & \Rightarrow u=\dfrac{\upsilon }{3} \\
\end{align}$
So, the velocity of the car is found to be ${{v}_{s}}=\dfrac{\upsilon }{3}$ where $\upsilon $ is the velocity of sound. Therefore option c is the right choice.

Note:
While doing these types of problems, we must be very aware of sign convention. In this case, the source and the observer are moving in the same direction. So we took it as positive. If these velocities are in opposite directions, we must take one of them as positive and one as negative.