Question

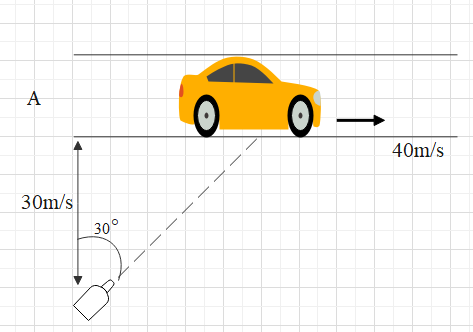
A racing car is travelling along a track at a constant speed of 40 m/s. A fixed T.V. camera is recording the event as shown in figure. In order to keep the car in view, in the position shown, the angular velocity of camera should be-
 

A. \[3rad/\operatorname{s}\]
B. \[2rad/\operatorname{s}\]
C. \[4rad/\operatorname{s}\]
D. \[1rad/\operatorname{s}\]

Answer 1

Hint: Consider the unknown distance and try to form an equation using trigonometry. Once the equation is formed then differentiate the equation formed and substitute the given values in the formula. Speed and velocity can be easily calculated this way.

Formula used: \[\tan \theta =\dfrac{Perpendicular}{base}\]

Complete step by step answer:
According to the question, the car is travelling with velocity 40m/s and the car is making an angle \[30{}^\circ \] with the camera. The figure below shows a systematic representation of the distance assumed.
Given-
\[
   {{v}_{car}}=40m/s \\
  \theta =30{}^\circ \\
\]

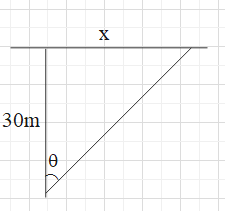
By using trigonometric formula we know,
 \[\tan \theta =\dfrac{Perpendicular}{base}\]
Therefore, from the above figure it is clear that \[x=30\tan \theta \]……..(1)
As we know definition of velocity is change in speed with respect to time which can be given as
\[v=\dfrac{dx}{dt}\]
Differentiating equation (1)
\[\left( \dfrac{dx}{dt} \right)=(30{{\sec }^{2}}\theta )\dfrac{d\theta }{dt}\]
\[\dfrac{d\theta }{dt}\] is the angular velocity i.e. change in angle with respect to time which can also be represented as \[\omega \].
Now velocity of car can also be written as \[{{v}_{car}}=(30{{\sec }^{2}}\theta )\omega \]
Rearranging the terms
\[ \omega =\dfrac{{{v}_{car}}}{30{{\sec }^{2}}\theta } \\
 =\dfrac{40}{30{{\sec }^{2}}30{}^\circ } \\
  =1rad/\operatorname{s}
\]
Therefore the angular velocity of the camera is found to be \[1rad/\operatorname{s}\].

So, the correct answer is “Option D”.

Additional Information: Angular velocity can be explained as how fast or slow an object rotates or revolves with respect to some point. In other words angular velocity is the rate of change of an angle.

Note: Always remember all the trigonometric functions and its value, as it can be used in solving problems in a much easier way. It is also necessary to remember the derivative of a given function. Like differentiating speed with time we get velocity, differentiating velocity with time we get acceleration and so on. Free body diagrams can also be drawn to understand the question clearly.