Question

A quadrant shaped flower bed is made of radius $ 14 $ meters in a square garden of side $ 100 $ meters in all the four corners. Find the area of the remaining part of the square garden.

Answer 1

Hint: Calculate the total area of the rectangle and the area of $ 4 $ sectors. Their difference will be the remaining area which is the required result.

Complete step-by-step answer:
Observe the diagram,

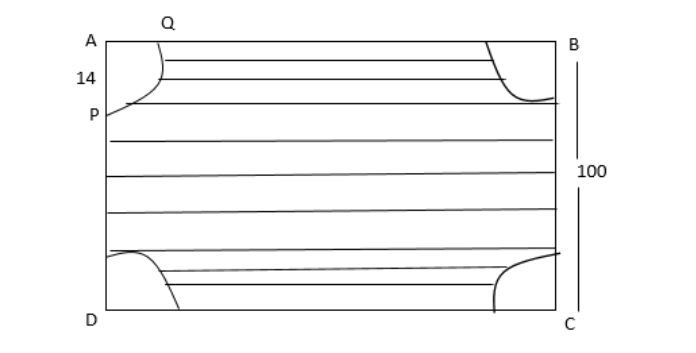
Let $ ABCD $ be the square garden with side $ a. $
Then, $ a = 100m $
Let $ a $ quadrant shaped flower bed is made in all four corners.
Let the radius of the flower beds be $ r $
Then, $ r = 14m $
Now, the area of the remaining part will clearly be the difference between the total area and the area of $ 4 $ flower beds.
Total area, $ T $ is the area of square as the garden is in square shape.
 $ \Rightarrow {T_t} = {a^2} $
It is given to us that $ a = 100m $
 $ \therefore {T_t} = {100^2}{m^2} $
Now, we know that a quadrant is one fourth of a circle.
Therefore, the area of $ 1 $ flower bed is equal to $ \dfrac{1}{4} $ area of the circle.
Hence, all the flower beds are of the same radius, all of them will have the same area.
Therefore, the area of $ 4 $ flower beds is equal to $ 4 $ times the area of one flower bed. Which is equal to $ 4 $ times $ \dfrac{1}{4} $ of the area of the circle.
That is equal to the area of $ 1 $ circle.
 $ = \pi {r^2} $
Where, $ r $ is the radius of the circle.
It is given that the radius.
The area of $ 4 $ flower beds. $ {T_f} $ is
 $ {T_t} = \pi \times {14^2} $
 $ {T_t} = \dfrac{{22}}{7} \times 14 \times 14 $
Therefore, the required area is
 $ = {T_t} - {T_f} $
 $ = 10000 - 22 \times 2 \times 14 $
 $ = 9384{m^2} $
Hence, the area of the remaining part of the square garden is $ 9384{m^2} $

Note: $ 1 $ quadrant $ = \dfrac{1}{4} $ circle
 $ 4 $ quadrant $ = 4 \times \dfrac{1}{4} $ circle
 $ 4 $ quadrant $ = 1 $ circle.
That is why, we calculated the area of $ 1 $ circle and calculated the area of $ 4 $ flower beds. It helps save time for calculation.