Question

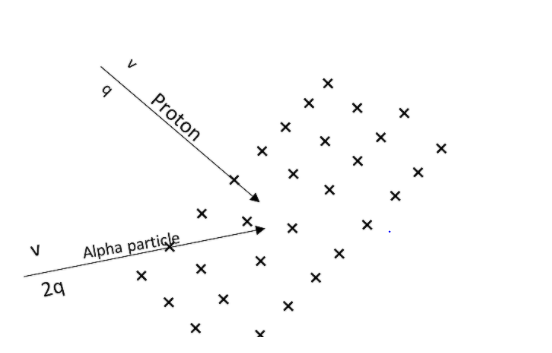
A proton and a $\alpha \text{ particle}$ moving with the same speed enter a uniform magnetic field. The proton enters perpendicular to the field. The magnetic force $F$ on the particles will be equivalent when the direction of motion of a particle is given as,
A. Parallel to the field
B. Perpendicular to the field
C. At $30{}^\circ $to the field
D. At $60{}^\circ $to the field

Answer 1

Hint: The power radiated by the black body is found by taking the product of the area of the black body, Stefan’s constant and the fourth power of temperature. The area is given as the area of a sphere as the black body is given as a spherical one. Now the conditions of halving the radius and making the temperature doubled, should be applied in the same equation and compare it with the previous condition. These all will help you to solve this question.

Complete step by step answer:
As we all know, the magnetic force acting due to the charged particle moving across a uniform magnetic field is given as,
$F=qvB\sin \theta $
As the angle between the field and velocity vector of a proton is given as,
$\theta =90{}^\circ $
Substituting this in the equation will give,
${{F}_{1}}=qvB$
Now let us calculate the magnetic force due to a $\alpha \text{ particle}$. As the charge of an $\alpha \text{ particle}$is given as the twice of the charge of a proton, we can write that,
$q=2q$
Substituting this in the equation will give,
${{F}_{2}}=2qvB\sin \theta $
As it is mentioned in the question that the magnetic force are equal, we can compare both the equations,
$qvB=2qvB\sin \theta $
Cancelling the common terms in the equation,
$\sin \theta =\dfrac{1}{2}$
From this we can calculate the angle of the direction of motion is,
$\theta =30{}^\circ $
Therefore the correct answer is option C.

Note:
Magnetic force is defined as the force of repulsion or attraction between the electrically charged particles due to the motion. It is the fundamental force which causes the action of electric motors and the magnetic attraction for iron. This is a vector quantity as well.