Question

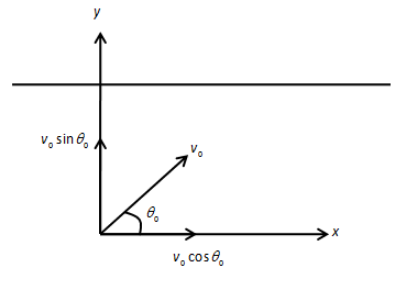
A projectile of mass m is fired into a liquid at an \[{\theta _0}\] with an initial velocity \[{v_0}\] as shown. If the liquid develops a frictional or drag resistance on the projectile which is proportional to its velocity, i.e., \[F = - kv\] where k is a positive constant, determine the x and y components of its velocity at any instant. Also find the maximum distance \[{x_{\max }}\] that it travels.
 

Answer 1

Hint: Use Newton’s second law of motion to determine the x and y component of acceleration produced by the net force in the projectile. We know that acceleration is the rate of change of velocity with respect to time. Use this concept and integrate the equation from initial velocity to final velocity for both x and y components simultaneously.

Formula used:
Newton’s second law,
\[F = ma\], where, m is the mass and a is the acceleration.
The instantaneous acceleration is,
\[a = \dfrac{{dv}}{{dt}}\]

Complete step by step answer:
We have given, the drag force due to liquid is, \[F = - kv\]. Since the velocity of projectile has both x and y components, we can write the drag force in the form of its x and y components as follows,
\[{F_x} = - k{v_x}\] …… (1)
\[{F_y} = - k{v_y}\] …… (2)

According to Newton’s second law, \[{F_{net}} = ma\]. Therefore, we write equation (1) as follows,
\[m{a_x} = - k{v_x}\]
 \[{a_x} = \dfrac{{ - k{v_x}}}{m}\] …… (3)
Here, \[{a_x}\] is the x component of acceleration.
Substitute \[\dfrac{{d{v_x}}}{{dt}}\] for \[{a_x}\] in the above equation.
\[\dfrac{{d{v_x}}}{{dt}} = \dfrac{{ - k{v_x}}}{m}\]
\[ \Rightarrow \dfrac{{d{v_x}}}{{{v_x}}} = \dfrac{{ - k}}{m}dt\]

We integrate the above equation from \[{v_0}\cos {\theta _0}\] (x component of initial velocity) to \[{v_x}\] (x component of final velocity).
 \[\int\limits_{{v_0}\cos {\theta _0}}^{{v_x}} {\dfrac{{d{v_x}}}{{{v_x}}}} = \int\limits_0^t {\dfrac{{ - k{v_x}}}{m}dt} \]
\[ \Rightarrow \ln \left( {{v_x}} \right)_{{v_0}\cos {\theta _0}}^{{v_x}} = \dfrac{{ - kt}}{m}\]
\[ \Rightarrow \ln \left( {{v_x} - {v_0}\cos {\theta _0}} \right) = \dfrac{{ - kt}}{m}\]
\[ \Rightarrow \ln \left( {\dfrac{{{v_x}}}{{{v_0}\cos {\theta _0}}}} \right) = \dfrac{{ - kt}}{m}\]
\[ \Rightarrow {v_x} = {v_0}\cos {\theta _0}{e^{\dfrac{{ - kt}}{m}}}\] …… (4)

In the vertical direction, the gravitational force also affects the motion of projectile. Therefore, the net acceleration of the projectile in vertical direction is,
\[{a_y} = - \dfrac{k}{m}{v_y} - g\]
Here, g is the acceleration due to gravity.
Substitute \[\dfrac{{d{v_y}}}{{dt}}\] for \[{a_y}\] in the above equation.
\[\dfrac{{d{v_y}}}{{dt}} = \dfrac{{ - k{v_y}}}{m} - g\]
\[ \Rightarrow \dfrac{{d{v_y}}}{{\dfrac{k}{m}{v_y} + g}} = - dt\]

Integrate the above equation from \[{v_0}\sin {\theta _0}\] (y component of initial velocity) to \[{v_y}\] (y component of final velocity).
\[\int\limits_{{v_0}\sin {\theta _0}}^{{v_y}} {\left( {\dfrac{{d{v_y}}}{{\dfrac{k}{m}{v_y} + g}}} \right)} = - \int\limits_0^t {dt} \]
\[ \Rightarrow \left[ {\dfrac{{\ln \left( {\dfrac{k}{m}{v_y} + g} \right)}}{{\dfrac{k}{m}}}} \right]_{{v_0}\sin {\theta _0}}^{{v_y}} = - t\]
\[ \Rightarrow \ln \left[ {\dfrac{{\left( {\dfrac{k}{m}{v_y} + g} \right)}}{{\dfrac{k}{m}\left( {{v_0}\sin {\theta _0}} \right) + g}}} \right] = - \dfrac{k}{m}t\]

Rearrange the above equation for \[{v_y}\] as follows,
\[{v_y} = \dfrac{m}{k}\left[ {\left( {\dfrac{k}{m}\left( {{v_0}\sin {\theta _0}} \right) + g} \right){e^{ - kt/m}} - g} \right]\]
This is the y-component of initial velocity.
Now the displacement or maximum horizontal distance of the projectile is,
\[dx = {v_x}dt\]
Substitute equation (4) in the above equation.
\[dx = \left( {{v_0}\cos {\theta _0}{e^{\dfrac{{ - kt}}{m}}}} \right)dt\]

Integrate the distance from o to x and velocity from 0 to t.
\[\int\limits_0^x {dx} = \int\limits_0^t {\left( {{v_0}\cos {\theta _0}{e^{\dfrac{{ - kt}}{m}}}} \right)} dt\]
\[ \Rightarrow x = {v_0}\cos {\theta _0}\left( {\dfrac{{{e^{\dfrac{{ - kt}}{m}}}}}{{\dfrac{{ - k}}{m}}}} \right)_0^t\]
\[ \Rightarrow x = \dfrac{{m{v_0}\cos {\theta _0}\left( {1 - {e^{ - kt/m}}} \right)}}{k}\]
The horizontal displacement will be a maximum when the term \[{e^{ - kt/m}}\] is zero.

Therefore, the maximum distance \[{x_{\max }}\] is, \[{x_{\max }} = \dfrac{{m{v_0}\cos {\theta _0}}}{k}\].


Note:Note that, we have used definite integrals. Therefore, the constant of integration C vanishes. While solving such types of questions where we need to calculate the integration of the function, the limits of integration is a crucial part. If you integrate the horizontal component of velocity of the body, then limits of integration should be the initial horizontal component of velocity to the final horizontal component of velocity. We know that the acceleration due to gravity does not affect the horizontal motion of the projectile. Therefore, in the horizontal direction, only the x component of drag force is acting on the projectile.