Question

A projectile is thrown into a space so as to have maximum horizontal range R. Taking the point of projection as origin, find out the coordinates of the point where the speed of the particle is minimum.
(A). $\left( \dfrac{\text{R}}{\text{2}}\text{, }\dfrac{\text{R}}{\text{4}} \right)$
(B). $\left( \dfrac{\text{R}}{\text{3}}\text{, }\dfrac{\text{R}}{\text{4}} \right)$
(C). $\left( \dfrac{\text{R}}{2}\text{, }\dfrac{\text{R}}{2} \right)$
(D). $\left( \dfrac{\text{R}}{3}\text{, }\dfrac{\text{R}}{2} \right)$

Answer 1

Hint: In order to answer this question, we should be having an idea about the concept of horizontal projectile. We should be knowing the idea of projectile motion. The diagram for this kind of numerical is very important. The coordinates required as an answer for this question can only be achieved by the drawing.

Complete step-by-step solution -
Let us first understand the meaning of horizontal range of a projectile. By horizontal range of projectile we mean, the horizontal displacement of a projectile, in case of the displacement of the projectile in the y - direction is zero. The following diagram demonstrates the question.

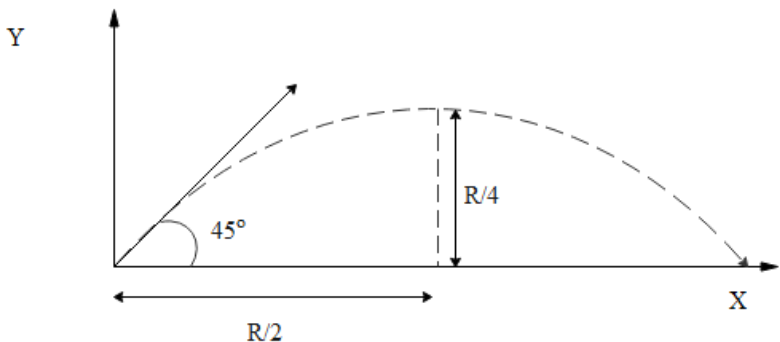
We know that the maximum horizontal range is denoted by $\text{R = 4H}\cdot \text{cot }\!\!\theta\!\!\text{ }$ where $\text{ }\!\!\theta\!\!\text{ = 45}{}^\circ$
This is because maximum horizontal range is achieved with an angle of inclination of $\text{45}{}^\circ$.
$\therefore \text{ R = 4H cot 45}{}^\circ$
$\Rightarrow \text{ R = 4H }\left[ \because \text{ cot 45}{}^\circ \text{ = 1} \right]$
We know that the speed of particles will be lowest at the highest point in the projectile.
Therefore, we can determine the highest point of the projectile with the coordinates $\left( \dfrac{\text{R}}{\text{2}}\text{, }\dfrac{\text{R}}{\text{4}} \right)$ as given in the diagram above.
Therefore, the correct option is Option A.

Note: Projectile motion is defined as a motion which is performed by any object or particle when it is projected near the surface of the Earth. The particle moves along the curved path on experiencing gravity.