Question

A projectile is given an initial velocity of $\hat i + 2\hat j$. Find the cartesian equation of its path. Take $g = 10{\text{m}}{{\text{s}}^{ - 2}}$.
A) $y = x - 5{x^2}$
B) $y = 2x - 5{x^2}$
C) $y = 2x - 15{x^2}$
D) $y = 2x - 25{x^2}$

Answer 1

Hint: The given initial velocity of the projectile has an x component and a y component. So the displacement of the projectile must have a horizontal component and a vertical component. The trajectory of the projectile can then be considered to be parabolic in nature. Newton’s first equation of motion for the displacement in the y-direction will give the equation of the trajectory of the projectile.

Formula used:
Newton’s first equation of motion is given by, $s = ut + \dfrac{1}{2}a{t^2}$ where $s$ is the displacement of the body, $u$ is its initial velocity, $t$ is the time taken and $a$ is its acceleration.
The equation of the trajectory of a projectile is given by, $y = x\tan \theta - \dfrac{1}{2}g\left( {\dfrac{{{x^2}}}{{{u_x}^2}}} \right)$ where $y$ is its vertical displacement, $x$ is its horizontal displacement, $\theta $ is the angle made by the projectile as it is thrown, $g$ is the acceleration due to gravity and ${u_x}$ is the x-component of its initial velocity.

Complete step by step answer:
Step 1: List the x-component and y-component of the given initial velocity.
The initial velocity of the projectile is given to be $\vec u = \hat i + 2\hat j$.
Then the x-component of the initial velocity will be ${u_x} = 1$ and its y-component is ${u_y} = 2$ .
Let $x$ be the displacement of the projectile along the x-direction.
Let $y$ be the displacement of the projectile along the y-direction.
Step 2: Using Newton’s first equation of motion to express the displacement of the projectile in the x-direction and the y-direction.
Newton’s first equation of motion gives the horizontal displacement of the projectile as $x = {u_x}t + \dfrac{1}{2}{a_x}{t^2}$
where $t$ is the time taken and ${a_x}$ is its acceleration in the x-direction.
For a projectile, the velocity in the x-direction remains constant.
$ \Rightarrow {a_x} = 0$
Thus we have $x = {u_x}t$ and on substituting for ${u_x} = 1$ we get, $x = 1 \times t = t$.
So the displacement along the horizontal direction is $x = t$
Similarly, the displacement of the projectile in the y-direction will be $y = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$ where $t$ is the time taken and ${a_y}$ is its acceleration in the y-direction.
For a projectile, the acceleration in the y-direction is given by the acceleration due to gravity.
$ \Rightarrow {a_y} = - g$
Thus we have $y = {u_y}t - \dfrac{1}{2}g{t^2}$ ----------- (1)
Substituting for $t = x$, ${u_y} = 2$ and $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ in equation (1) we get,
$\Rightarrow y = 2x - \dfrac{1}{2}10{x^2}$.
Simplifying we get,
$\Rightarrow y = 2x - 5{x^2}$ .

Thus the equation of the trajectory of the projectile is $y = 2x - 5{x^2}$. So the correct option is B.

Note:
Alternate method
The projectile can be considered to make an angle $\theta $ with the x-axis as it moves with the initial velocity $\vec u = \hat i + 2\hat j$. We have ${u_x} = 1$ and ${u_y} = 2$ as the x-component and y-component of the initial velocity. The projection of the projectile is shown in the figure below.

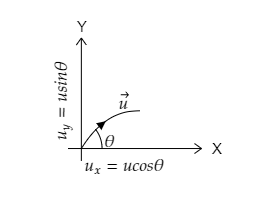
From the figure, the x-component and y-component of the initial velocity are given by. ${u_x} = u\cos \theta = 1$ and ${u_y} = u\sin \theta = 2$ respectively.
Let $x$ and $y$ be the displacements of the projectile along the x-direction and y-direction respectively.
Then the equation of the trajectory of the projectile is generally expressed as
$y = x\tan \theta - \dfrac{1}{2}g\left( {\dfrac{{{x^2}}}{{{u_x}^2}}} \right)$ --------- (A)
We have $\tan \theta = \dfrac{{u\cos \theta }}{{u\sin \theta }} = \dfrac{2}{1} = 2$.
Then substituting for $\tan \theta = 2$, ${u_x} = 1$ and $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ in equation (A) we get,$y = 2x - \dfrac{1}{2}10\left( {\dfrac{{{x^2}}}{{{1^2}}}} \right)$
$ \Rightarrow y = 2x - 5{x^2}$ .

Thus the equation of the trajectory is $y = 2x - 5{x^2}$.