Question

A prism of refractive index $\sqrt{2}$ has a refracting angle of ${{60}^{\circ }}$. At what angle a ray must be incident on it so that it suffers a minimum deviation.
A. ${{45}^{\circ }}$
B. ${{60}^{\circ }}$
C. ${{90}^{\circ }}$
D. ${{180}^{\circ }}$

Answer 1

Hint: At the angle of minimum deviation, the angle of incidence will be equal to the angle of emergence. We are given that the refractive index of the prism is $\sqrt{2}$ and the angle of the prism is given ${{60}^{\circ }}$. So, keeping the mentioned points in mind, we can calculate the angle of incidence by using the formula for the refractive index of the prism.
Formula Used:
The refractive index of the prism is given by,
$\mu =\dfrac{\sin \left[ \dfrac{A+{{\delta }_{m}}}{2} \right]}{\sin \left[ \dfrac{A}{2} \right]}$

Complete step by step answer:

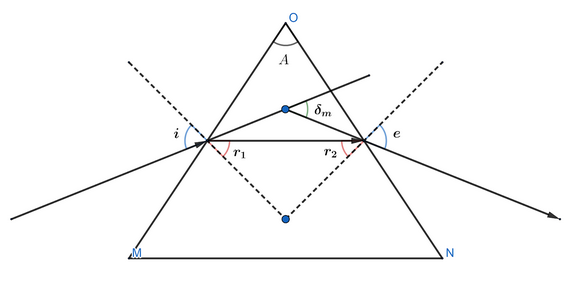
At the minimum deviation, the angle of incidence of light is equal to the angle of emergence, $i=e$. So we can write,
$i+e=A+{{\delta }_{m}}$
$\Rightarrow i=\left[ \dfrac{A+{{\delta }_{m}}}{2} \right]$ …. Equation (1)
We know that the formula for the refractive index of the prism is given by,
$\mu =\dfrac{\sin \left[ \dfrac{A+{{\delta }_{m}}}{2} \right]}{\sin \left[ \dfrac{A}{2} \right]}$…. Equation (2)
Comparing equation (1) and (2), we get,
$\mu =\dfrac{\sin \left( i \right)}{\sin \left[ \dfrac{A}{2} \right]}$
$\Rightarrow \sin \left( i \right)=\mu \times \sin \left[ \dfrac{A}{2} \right]$
Substituting the values in the above equation we get,
$\sin \left( i \right)=\sqrt{2}\times \sin \left[ \dfrac{{{60}^{\circ }}}{2} \right]$
$\sin \left( i \right)=\sqrt{2}\times \sin \left[ {{30}^{\circ }} \right]$
$\Rightarrow i={{\sin }^{-1}}\left[ \dfrac{1}{\sqrt{2}} \right]$
$\therefore i={{45}^{\circ }}$
So, the angle of incidence for minimum deviation is ${{45}^{\circ }}$.
So, the answer to the question is option (A).
Note:
The refractive index of a material is a function of wavelength. So for each wavelength of light, there will be a refractive index for each of them. So, when white light passes through a prism, it gets split into it its constituent colours because each wavelength will have a refractive index and as a result of different speeds while passing through the same medium. This phenomenon is called the dispersion of light.
When a ray of light is incident on an equilateral prism surface, the light ray will bend towards the normal, since the light is passing from a rarer medium to a denser medium. When the same ray hits the other side and comes out of the prism, the emergent ray will bend away from the normal. This phenomenon is known as refraction of light.