Question

A potentiometer wire of length 10m and resistance 10$\Omega $per meter is connected in series with a resistance box and a 2 volts battery. If a potential difference of 100mV is balanced across the whole length of potentiometer wire, then the resistance introduced in the resistance box will be:
$
  (a){\text{ 1900}}\Omega \\
  (b){\text{ 900}}\Omega \\
  (c){\text{ 190}}\Omega \\
  (d){\text{ 90}}\Omega \\
$

Answer 1

Hint –In this question let the resistance of the resistance box be R’. Calculate the value of resistance of the whole potentiometer wire and apply ohm’s law to find the total amount of current flowing through the potentiometer wire. Then apply K.V.L in the circuit (see figure). This will help to find the value of R’.
Step by step answer:

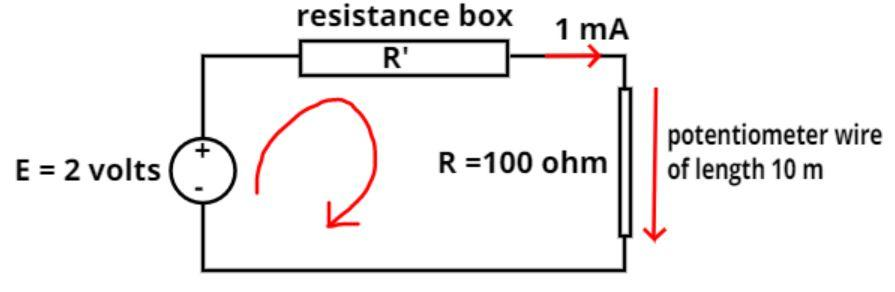
Given data:
Length of the potentiometer wire = 10 m.
And it is given that resistance of the wire is 10$\Omega $per meter.
So the resistance (R) of the whole wire = $10 \times 10 = 100$$\Omega $
Now it is given that the potential difference (V) of the whole wire is 100mV.
So according to Ohm’s law V=IR, where I = current in the wire.
Now substitute the values in this equation we have,
$ \Rightarrow 100mV = I \times 100$
$ \Rightarrow I = 1$mA.
As we know that 1mA = $1 \times {10^{ - 3}}$A
Therefore, $I$ = $1 \times {10^{ - 3}}$A
Now it is given that a resistance box and a 2 volt battery is connected in series with this potentiometer wire as shown in the figure.
Let E = 2 volts
And, let the resistance of the resistance box be R’.
Now as we know that in series the current remains.
So apply K.V.L in the circuit diagram we have,
$ \Rightarrow E - I\left( {R + R'} \right) = 0$
Now substitute the values in this equation we have,
$ \Rightarrow 2 - 1 \times {10^{ - 3}}\left( {100 + R'} \right) = 0$
Now simplify this equation we have,
$ \Rightarrow 2 = 1 \times {10^{ - 3}}\left( {10 + R'} \right)$
$ \Rightarrow 100 + R' = \dfrac{2}{{1 \times {{10}^{ - 3}}}} = 2000$
$ \Rightarrow R' = 2000 - 100 = 1900\Omega $
So this is the required resistance of the resistance box.
So this is the required answer.
Hence option (A) is the correct answer.

Note – Kirchhoff’s voltage law and Kirchhoff’s current law is very helpful in solving problems of this kind. KVLl states that the total potential inside a closed circuit will always be equal to the potential drop across the various elements present inside that circuit. KCL states that the total current incoming at a certain node will always be equal to the total current outgoing through that node.