Question

A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situated at a distance of 2m from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is 19.6cm from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationary goli without falling on the ground earlier?

Answer 1

Hint: In such questions we have to draw the geometry of the question to understand what is happening. The distance between first and second player is 2m and goli is being projected horizontally from a height of 19.6cm, so we have drawn that in the following diagram.to find the speed we are going to use equations of motion.

Complete step by step solution:

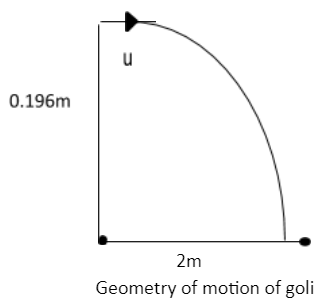
Given,
Height from which goli was thrown\[s = 19.6{\text{ cm}}\]
$s = 0.196{\text{ m}}$
Horizontal distance between golis $x = 2{\text{ m}}$
Acceleration due to gravity $g = 9.8{\text{ m/}}{{\text{s}}^2}$
Let the speed by which the goli is being thrown is u. The horizontal component of speed is \[{u_x}\] and the vertical component is \[{u_y}\].
The vertical component of speed \[{u_y} = 0\]
Using the equation of motion for vertical component
$\Rightarrow s = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$
Putting the values of $s,{u_y},\operatorname{t} {\text{and }}{a_y}$
$\Rightarrow 0.196 = 0 + \dfrac{1}{2} \times 9.8{t^2}$
$\Rightarrow {t^2} = \dfrac{{0.196 \times 2}}{{9.8}}$
Finding the time taken by goli to reach the other goli,
$\Rightarrow {t^2} = \dfrac{{0.392}}{{9.8}}$
$\Rightarrow {t^2} = 0.04$
$\Rightarrow t = 0.2{\text{ s}}$
Now using the equation of motion in horizontal direction,
$\Rightarrow x = {u_x}t + \dfrac{1}{2}{a_x}{t^2}$
The acceleration in x direction is 0.
Putting the values of $x,\operatorname{t} {\text{and }}{a_x}$
$\Rightarrow 2 = {u_x} \times 0.2 + \dfrac{1}{2} \times 0 \times {(0.2)^2}$
$\Rightarrow 2 = {u_x} \times 0.2$
The speed of goli to reach the other goli,
$\Rightarrow {u_x} = \dfrac{2}{{0.2}}$
$\Rightarrow {u_x} = 10{\text{ m/s}}$

The speed of goli by which it should be projected is ${u_x} = 10{\text{ m/s}}$.

Note: Goli was thrown in a horizontal direction from a height s, so we have to be careful that we have to find both horizontal and vertical components of the speed of goli. We have to be careful that the acceleration due to gravity is zero in the horizontal direction. Since the goli was moving in a downward vertical direction so the value of acceleration due to gravity is positive. We have to be careful while using the equations of motion. Since we know that there are three equations of motion, we have to decide carefully which equation we should use to solve the question.