Question

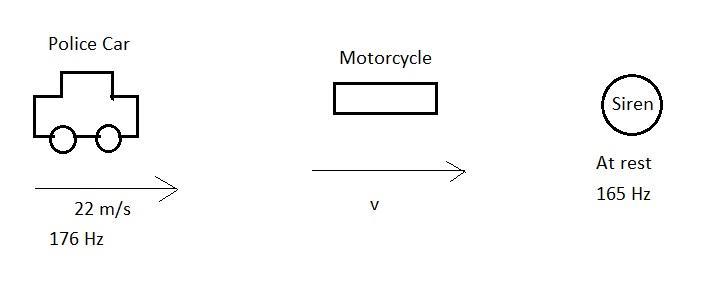
A police car moving at \[22\,{\text{m/s}}\] chases a motorcyclist. The policeman sounds his horn at \[176\,{\text{Hz}}\] , while both of them move towards a stationary siren of frequency \[165\,{\text{Hz}}\] . Calculate the speed of the motorcycle, if it is given that he does not observe any beats:

A. \[33\,{\text{m/s}}\]
B. \[22\,{\text{m/s}}\]
C. Zero
D. \[11\,{\text{m/s}}\]

Answer 1

Hint: We will use Doppler’s equation for the two cases. Since the question suggests that no beat is to be observed, so the two apparent frequencies will be the same. We will compare the two equations and manipulate accordingly.

Complete step by step answer:

In the given problem, we are supplied the following data:
The velocity of the police car is \[22\,{\text{m/s}}\] .
Frequency of the sound emitted by the police car is \[176\,{\text{Hz}}\] .
Frequency of the sound emitted by the siren is \[165\,{\text{Hz}}\] .
Speed of sound in the air medium is \[330\,{\text{m/s}}\] .

In this case, both the motorcyclist and the police are moving in the same direction towards the siren. The police car is moving behind the motorcycle. The motorcycle is going away from the source.
The apparent frequency of the horn as heard by the motorcyclist is given by the Doppler’s equation:
\[n' = {n_c}\left( {\dfrac{{v - {v_m}}}{{v - {v_c}}}} \right)\] …… (1)
Where,
\[n'\] indicates apparent frequency heard by the motorcyclist.
\[{n_c}\] indicates frequency of the sound emitted by the police car.
\[v\] indicates the velocity of the sound in air.
\[{v_m}\] indicates the velocity of the motorcyclist.
\[{v_c}\] indicates the velocity of the police car.

Now, we substitute the required values in the equation (1), and we get:
\[n' = 176\left( {\dfrac{{330 - {v_m}}}{{330 - 22}}} \right)\]
\[n' = 176\left( {\dfrac{{330 - {v_m}}}{{308}}} \right)\] …… (2)

In the second case,
The motorcycle is approaching the siren while the siren is stationary.
The apparent frequency of the siren as heard by the motorcyclist is given by the Doppler’s equation:
\[n'' = {n_s}\left( {\dfrac{{v + {v_m}}}{{v + {v_s}}}} \right)\] …… (3)
Where,
\[n''\] indicates the apparent frequency of the siren as heard by the motorcyclist.
\[{n_s}\] indicates the frequency of the siren.
\[{v_m}\] indicates the velocity of the motorcyclist.
\[{v_s}\] indicates the velocity of the police car.
\[v\] indicates the velocity of the sound in air.

Now, we substitute the required values in the equation (3), and we get:
\[n'' = {n_s}\left( {\dfrac{{v + {v_m}}}{{v + {v_s}}}} \right)\]
$ \implies n'' = 165\left( {\dfrac{{330 + {v_m}}}{{330 + 0}}} \right) $
$ \implies n'' = 165\left( {\dfrac{{330 + {v_m}}}{{330}}} \right) $ …… (4)

We know, there occurs no beats when the frequencies of the two sources are equal in magnitude. So, the difference between the frequencies between the two sources is zero.
\[n' - n'' = 0\]
\[n' = n''\] …… (5)

Now we use equations (2) and (4) in equation (5), and we get:
$ 176\left( {\dfrac{{330 - {v_m}}}{{308}}} \right) = 165\left( {\dfrac{{330 + {v_m}}}{{330}}} \right) \\ $
$ \dfrac{{330 - {v_m}}}{{330 + {v_m}}} = \dfrac{{165}}{{176}} \times \dfrac{{308}}{{330}} \\ $
$ \implies \dfrac{{330 - {v_m}}}{{330 + {v_m}}} = \dfrac{7}{8} \\ $
$ \implies {v_m} = 22\,{\text{m/s}} \\ $
Hence, the speed of the motorcycle is \[22\,{\text{m/s}}\] .

So, the correct answer is “Option B”.

Note:
While solving this problem, the direction of the objects should be kept in mind. The direction corresponds to the signs used in the equations. When the waves differ in the frequencies, then there are constructive and destructive interferences which are alternating in nature, leading the sound to be heard loud and soft alternatively.