Question

A pole is slightly inclined towards the east. At two points due west of it at distances $a\,\,and\,\,b$, the angle of elevation of the top of the pole are \[\alpha \,\,and\,\,\beta \] respectively. The inclination of the pole to the horizon is:
A. ${\tan ^{ - 1}}\left[ {\dfrac{{a + b}}{{b\cot \alpha - \cot \beta }}} \right]$
B. ${\tan ^{ - 1}}\left[ {\dfrac{{b - a}}{{b\cot \alpha - acot\beta }}} \right]$
C. ${\cos ^{ - 1}}\left[ {\dfrac{{a - b}}{{b\cos \alpha - \cos \beta }}} \right]$
D. ${\sin ^{ - 1}}\left[ {\dfrac{{a - b}}{{b\cot \alpha - a\cot \beta }}} \right]$

Answer 1

Hint: Firstly, we will make a diagram according to the information in the question. Thereafter, we will solve and find the value of $c$and $h$, then find the inclined angle to get the answer.

Complete step-by-step answer:

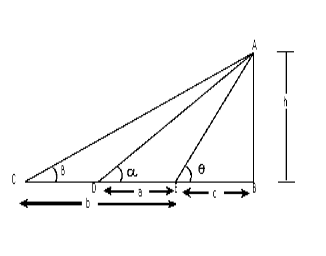
Let $AB$ be a pole $C\,\,and\,\,D$ are the points from where it is observed.
Let $AB = h,\,\,BE = c$
Here, $ED = a\,\,and\,\,EC = b$
Now, in$\Delta ABD,\,\,at\,\,\angle B = {90^o}$, by using trigonometric ratio, we have
$
  tan\alpha = \dfrac{{AB}}{{BD}} \\
  \tan \alpha = \dfrac{{AB}}{{BE + ED}} \\
 $
We will substitute the value of $AB = h,\,\,BE = c$and $ED = a\,$,we have
$\tan \alpha = \dfrac{h}{{a + c}}$
\[(a + C)\tan \alpha = h\] …..(i)
Similarly, in $\Delta ABC,\,\,at\,\,\angle \beta = {90^{}}O$, so by using trigonometric ratio we have
$
  tan\beta = \dfrac{{AB}}{{BC}} \\
  \tan \beta = \dfrac{{AB}}{{BE + EC}} \\
 $
We will substitute the value of $AB = h,\,\,BE = c$and $EC = b$,we have
$\tan \beta = \dfrac{h}{{c + b}}$
\[(b + c)\tan \beta = h\] ……(ii)
Now, from equation (i) and (ii), we have
$(a + c)\tan \alpha = (b + c)\tan \beta $
$a\tan \alpha + c\tan \alpha = b\tan \beta + c\tan \beta $
$a\tan \alpha - b\tan \beta = c\tan \beta - c\tan \alpha $
$a\tan \alpha - b\tan \beta = c(\tan \beta - \tan \alpha )$
$ \Rightarrow c = \dfrac{{a\tan \alpha - b\tan \beta }}{{\tan \beta - \tan \alpha }}$ …….(iii)
Now, we will substitute the value of $c$in equation (i), we have
$h = a\tan \alpha + c\tan \alpha $
\[h = \dfrac{{a\tan \alpha }}{1} + \tan \alpha \left( {\dfrac{{a\tan \alpha - b\tan \beta }}{{\tan \beta - \tan \alpha }}} \right)\]
Now, we will take LCM $\tan \beta - \tan \alpha ,$we have
$h = \dfrac{{a\tan \alpha (\tan \beta - \tan \alpha ) + \tan \alpha (a\tan \alpha - b\tan \beta )}}{{\tan \beta - \tan \alpha }}$
$h = \dfrac{{a\tan \alpha \tan \beta - a{{\tan }^2}\alpha + a{{\tan }^2}\alpha - b\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}$
$h = \dfrac{{a\tan \alpha \tan \beta - b\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}$
$h = \dfrac{{a\tan \alpha \tan \beta - b\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}$
Take $\tan \alpha \tan \beta $ common in the numerator, we have
$h = \dfrac{{\tan \alpha \tan \beta (a - b)}}{{\tan \beta - \tan \alpha }}$
Now, in $\Delta ABE$
$\tan \theta = \dfrac{{AB}}{{BE}}$
$\tan \theta = \dfrac{h}{c}$ …..(iv)
Now, we will substitute ion value of $h$ and $c$ in equation (iv) , we have
$\tan \theta = \dfrac{{\dfrac{{(a - b)\tan \alpha \tan \beta )}}{{\tan \beta - \tan \alpha }}}}{{\dfrac{{a\tan \alpha - b\tan \beta }}{{\tan \beta - \tan \alpha }}}}$
$\tan \theta = \dfrac{{(a - b)\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }} \times \dfrac{{tan\beta - \tan \alpha }}{{a\tan \alpha - b\tan \beta }}$
$\tan \theta = \dfrac{{(a - b)\tan \alpha \tan \beta }}{{(a\tan \alpha - btain\beta )}}$
\[\tan \theta = \dfrac{{ - (b - a)\tan \alpha \tan \beta }}{{ - (b\tan \beta - a\tan \alpha )}}\]
$\tan \theta = \dfrac{{(b - a)\tan \alpha \tan \beta }}{{b\tan \beta - a\tan \alpha }}$
Now, as we know that $\tan \theta = \dfrac{1}{{\cot \theta }}$
$\tan \theta = \dfrac{{(b - a)\dfrac{1}{{\cot \alpha }} \times \dfrac{1}{{\cot \beta }}}}{{\left( {\dfrac{b}{{\cot \beta }} - \dfrac{a}{{\cot \alpha }}} \right)}}$
$ \Rightarrow \tan \theta = \dfrac{{(b - a)\dfrac{1}{{\cot \alpha }} \times \dfrac{1}{{\cot \beta }}}}{{\left( {\dfrac{{b\cot \alpha - a\cot \beta }}{{\cot \beta \times \cot \alpha }}} \right)}}$
$ \Rightarrow \tan \theta = \dfrac{{(b - a)\dfrac{1}{{\cot \alpha }} \times \dfrac{1}{{\cot \beta }} \times \cot \beta \times \cot \alpha }}{{b\cot \alpha - a\cot \beta )}}$
$ \Rightarrow \tan \theta = \dfrac{{(b - a)}}{{b\cot \alpha - a\cot \beta }}$
$ \Rightarrow \theta = {\tan ^{ - 1}}\dfrac{{(b - a)}}{{b\cot \alpha - a\cot \beta }}$
So, the correct answer is “Option B”.

Note: Students remember that when you make an angle of elevation then follow this instruction it will help you. When you see an object above you, there is an angle of elevation between the horizontal and your line of sight to the object.