Answer
Verified432.6k+ views
Hint: In this question, are given a pole on a building with its dimensions. An observer is at the same level of the pole and its distance from the ground is 300m. The angle subtended by the pole and the building are the same i.e. $\theta $ . We need to find this angle using basic trigonometric function tan and then the distance of the observer from the top of the pole.
Complete step by step answer:
Let’s solve the problem now.
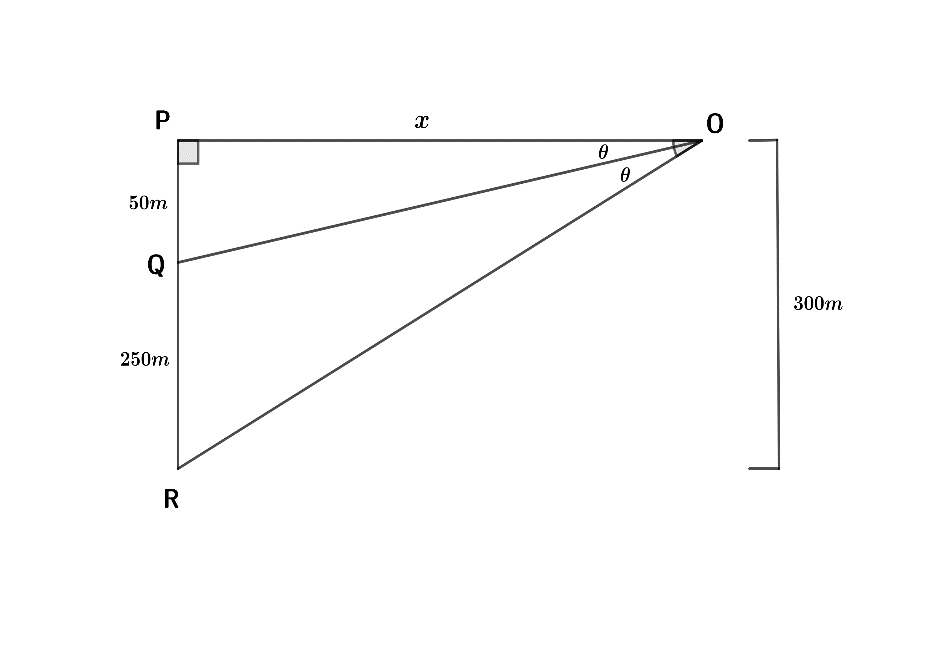
Draw the figure like this. Now, let’s see what all terms are given to understand the problem. Here, QR is a building of 250m on which there is a pole of 50m. There is an observer which is at the same level as the pole and standing 300m above from the ground. The building and the pole subtend the equal angle i.e. $\theta $. We let the distance from the pole to the observer as ‘x’ which needs to be find out. First of all we have to find the angle $\theta $.
For $\Delta OPQ$,
$\Rightarrow $PQ = 50m
$\Rightarrow $OP = x
So,
$\Rightarrow $tan$\theta $ = $\dfrac{perpendicular}{base}$
$\Rightarrow $tan$\theta $ = $\dfrac{50}{x}.....(i)$
Now, for $\Delta OPR$,
$\Rightarrow $PR = 50m + 250m = 300m
$\Rightarrow \Rightarrow $OP = x
And the angle will be twice because it will take the whole $\angle O$ in this case.
$\Rightarrow $tan2$\theta $ = $\dfrac{300}{x}......(ii)$
As we know that:
$\Rightarrow $tan2$\theta $ = $\dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }$
Now, put this value in the place of tan2$\theta $ in equation(ii), we get:
$\Rightarrow \dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }$ = $\dfrac{300}{x}$
Use equation(i) to put the value of tan$\theta $:
$\Rightarrow \dfrac{2\times \left( \dfrac{50}{x} \right)}{1-{{\left( \dfrac{50}{x} \right)}^{2}}}$ = $\dfrac{300}{x}$
Perform multiplication and squaring wherever necessary:
$\Rightarrow \dfrac{\dfrac{100}{x}}{1-\dfrac{2500}{{{x}^{2}}}}$ = $\dfrac{300}{x}$
Now, take denominator to the other side in the numerator:
$\Rightarrow \dfrac{100}{x}$ = $\dfrac{300}{x}\left( 1-\dfrac{2500}{{{x}^{2}}} \right)$
Reciprocate $\dfrac{300}{x}$ and take it to the other side:
$\Rightarrow \dfrac{100}{x}\times \dfrac{x}{300}$ = $\left( 1-\dfrac{2500}{{{x}^{2}}} \right)$
Cancel the like terms on the left hand side of the equation:
$\Rightarrow \dfrac{1}{3}$ = $\left( 1-\dfrac{2500}{{{x}^{2}}} \right)$
Now, subtract $\dfrac{1}{3}$ from 1:
$\Rightarrow \dfrac{2500}{{{x}^{2}}}$ = $1-\dfrac{1}{3}$
Solve the fraction:
$\Rightarrow \dfrac{2500}{{{x}^{2}}}$ = $\dfrac{2}{3}$
Now, keep ‘x’ alone:
$\Rightarrow \dfrac{3}{2}\times 2500={{x}^{2}}$
Multiply and reduce the terms:
$\Rightarrow \dfrac{7500}{2}={{x}^{2}}$
Take under root:
$\Rightarrow \sqrt{3750}=x$
Value of x is:
$\therefore x=25\sqrt{6}$m
This is the final answer.
Note: In these types of questions, don’t assume things and solve them. Diagrams are must to draw before solving. You should form equations for the given terms, which makes it easy to find the unknown values or angles. If options are not given, then solve the root also at the end so that marks cannot be deducted.
Complete step by step answer:
Let’s solve the problem now.
Draw the figure like this. Now, let’s see what all terms are given to understand the problem. Here, QR is a building of 250m on which there is a pole of 50m. There is an observer which is at the same level as the pole and standing 300m above from the ground. The building and the pole subtend the equal angle i.e. $\theta $. We let the distance from the pole to the observer as ‘x’ which needs to be find out. First of all we have to find the angle $\theta $.
For $\Delta OPQ$,
$\Rightarrow $PQ = 50m
$\Rightarrow $OP = x
So,
$\Rightarrow $tan$\theta $ = $\dfrac{perpendicular}{base}$
$\Rightarrow $tan$\theta $ = $\dfrac{50}{x}.....(i)$
Now, for $\Delta OPR$,
$\Rightarrow $PR = 50m + 250m = 300m
$\Rightarrow \Rightarrow $OP = x
And the angle will be twice because it will take the whole $\angle O$ in this case.
$\Rightarrow $tan2$\theta $ = $\dfrac{300}{x}......(ii)$
As we know that:
$\Rightarrow $tan2$\theta $ = $\dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }$
Now, put this value in the place of tan2$\theta $ in equation(ii), we get:
$\Rightarrow \dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }$ = $\dfrac{300}{x}$
Use equation(i) to put the value of tan$\theta $:
$\Rightarrow \dfrac{2\times \left( \dfrac{50}{x} \right)}{1-{{\left( \dfrac{50}{x} \right)}^{2}}}$ = $\dfrac{300}{x}$
Perform multiplication and squaring wherever necessary:
$\Rightarrow \dfrac{\dfrac{100}{x}}{1-\dfrac{2500}{{{x}^{2}}}}$ = $\dfrac{300}{x}$
Now, take denominator to the other side in the numerator:
$\Rightarrow \dfrac{100}{x}$ = $\dfrac{300}{x}\left( 1-\dfrac{2500}{{{x}^{2}}} \right)$
Reciprocate $\dfrac{300}{x}$ and take it to the other side:
$\Rightarrow \dfrac{100}{x}\times \dfrac{x}{300}$ = $\left( 1-\dfrac{2500}{{{x}^{2}}} \right)$
Cancel the like terms on the left hand side of the equation:
$\Rightarrow \dfrac{1}{3}$ = $\left( 1-\dfrac{2500}{{{x}^{2}}} \right)$
Now, subtract $\dfrac{1}{3}$ from 1:
$\Rightarrow \dfrac{2500}{{{x}^{2}}}$ = $1-\dfrac{1}{3}$
Solve the fraction:
$\Rightarrow \dfrac{2500}{{{x}^{2}}}$ = $\dfrac{2}{3}$
Now, keep ‘x’ alone:
$\Rightarrow \dfrac{3}{2}\times 2500={{x}^{2}}$
Multiply and reduce the terms:
$\Rightarrow \dfrac{7500}{2}={{x}^{2}}$
Take under root:
$\Rightarrow \sqrt{3750}=x$
Value of x is:
$\therefore x=25\sqrt{6}$m
This is the final answer.
Note: In these types of questions, don’t assume things and solve them. Diagrams are must to draw before solving. You should form equations for the given terms, which makes it easy to find the unknown values or angles. If options are not given, then solve the root also at the end so that marks cannot be deducted.