Question

A point z moves on the curve $|z - 4 - 3i| = 2$ in an argand plane. The maximum and minimum values of $|z|$ are-
A. 2, 1
B. 6, 5
C. 4, 3
D. 7, 3

Answer 1

Hint: The concept of complex numbers and the argand plane will be used in this problem. The square root of -1 is an imaginary number called iota and represented by the letter $‘i’$. An argand plane is a plane which represents these complex numbers in a graphical form, where the horizontal axis(X) represents the real part, and the vertical axis represents the imaginary part. The general equation of a circle in the argand plane is-
$|z - {z_o}| = r$, where ${z_o}$ is the centre and r is its radius.

Complete step-by-step solution-
We have been given the equation $|z - 4 - 3i| = 2$ in an argand plane. When we compare it with the general equation of a circle, we can see that-
${z_o} = 4 + 3i$
Hence, the coordinates of the center are $(4, 3)$.
Also, $r = 2$
The radius of the circle is 2 units.

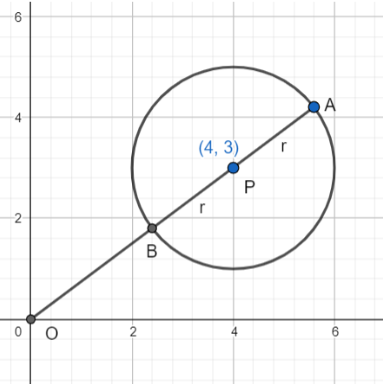
The point z lies on the circumference of the imaginary circle. The value of $|z|$ will be maximum when it is extended along line OP upto point A. Similarly, when we move in the opposite direction, the line OP cuts the circle at B, which will have the minimum value of $|z|$. Mathematically-
${\left| z \right|_{\max }} = OA = OP + r$
$\Rightarrow {\left| z \right|_{\min }} = OB = OP - r$
We know that the point P is represented by $4 + 3i$, so the magnitude of line OP can be calculated using the formula-
$\left| {{\text{a}} + ib} \right| = \sqrt {{{\text{a}}^2} + {{\text{b}}^2}} $.
$\Rightarrow OP = \left| {4 + 3{\text{i}}} \right| = \sqrt {{4^2} + {3^2}} = 5$.........(1)
Substituting the value of OP from equation (1) and r = 2,
${\left| z \right|_{\max }} = OP + r = 5 + 2 = 7$
$\Rightarrow {\left| z \right|_{\min }} = OP - r = 5 - 2 = 3$
These are the maximum and minimum values of $|z|$. The correct option is (D.) 7, 3.

Note: In such types of questions, identifying the equation and representing it graphically is the best method. If we did not know that the given equation is of an imaginary circle, the question would have become lengthy and calculative. So, we should remember the general equations of all conics and straight lines in the argand plane as well, as it helps in problem-solving. Also, we should keep in mind the various formulas related to the modulus of a complex number.