Question

A point traversed half a circle of radius $r$ during time interval ${t_0}$, then its mean speed and magnitude of mean velocity are:
A. $\dfrac{{\pi r}}{{{t_0}}},\dfrac{r}{{{t_0}}}$
B. $\dfrac{{2\pi r}}{{{t_0}}},\dfrac{{2r}}{{{t_0}}}$
C. $\dfrac{{\pi r}}{{{t_0}}},\dfrac{{2r}}{{{t_0}}}$
D. $\dfrac{{2\pi r}}{{{t_0}}},\dfrac{r}{{{t_0}}}$

Answer 1

Hint: When a particle traverses the half of the circle there will be a speed associated with it and this average speed is measured in terms of the distance travelled by the time taken to cover that distance. The velocity is measured in terms of the displacement of the particle by the total time taken. The formulas for these two quantities are applied in-order to determine the magnitude of the average speed and velocity of the particle.

Formula used:
The average speed is given by the formula:
$\text{speed} = \dfrac{d}{t}$
The average velocity of the particle is given by:
$v = \dfrac{\text{displacement}}{\text{time}}$
Where, $d$ is the total distance, $t$ is the total time taken and $v$ denotes the average velocity of the particle.

Complete step by step answer:
When a particle travels from one point to another there is a certain amount of speed or velocity associated with it. This average or the total speed and velocity taken by the same particle when it traverses across half of the path of a circle is to be determined.

In-order to find these quantities we must first know their concept. The average speed is defined to be the total distance travelled by the object divided by the total time taken to cover that distance. The average speed is always calculated for an object moving with variable speed. The equation for the average speed is given by the formula:
$\text{speed} = \dfrac{d}{t}$ ------($1$)
Where, $d$ represents the distance and $t$ represents the total time taken.

The average velocity of the particle is said to be the ratio of the total displacement of the particle by the time interval in which the displacement occurs. It is known as the average velocity because the velocity calculated is said to be an object that exhibits variable velocity that is there is a displacement associated and the calculation is done over a time interval or a time difference is taken. The average velocity of the particle is given by:
$v = \dfrac{\text{displacement}}{\text{time}}$ ------($2$)
The term average refers to the net or the total of the quantity that is considered since the body may move with variable motion so the total distance over the entire varying time interval is calculated.

The diagram for the particle which travels half the circle is given by the below diagram.

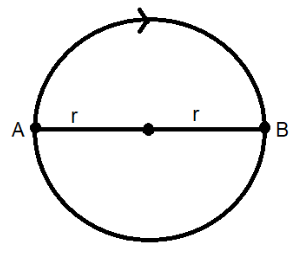
First we will calculate the speed of the particle. The particle, as per the question, is said to travel half the circle which means that the particle traverses the half of the arc of the circle. This will be the path or the route taken by the particle and hence this will be the total distance covered by the particle. The length of the circumference or the arc length of the entire circle is given by the formula:
$length = 2\pi r$
Here, $r$ is the radius of the circle as per the diagram. But here only half of the circle or the arc length is considered so the length will become:
$length = \dfrac{{2\pi r}}{2}$
$ \Rightarrow length = \pi r$
This length is said to be the distance covered by the particle. The time interval taken from the particle to travel this distance is given to be ${t_0}$. Hence we substitute the values in the equation ($1$)
$ \Rightarrow speed = \dfrac{{\pi r}}{{{t_0}}}$
Thus, the average velocity of the particle which travels half the circle has a magnitude equivalent to $\dfrac{{\pi r}}{{{t_0}}}$.

Next, we calculate the average velocity of the particle. The displacement is given by the difference between the initial and final points of the particle that is travelling regardless of the path. Displacement always chooses the shortest path to cover the distance when there is more than one path to get to the destination location. Hence, from the diagram we can see that the shortest path from point A to B is the straight line path. Hence the displacement will be:
$\text{length} = r + r$
$ \Rightarrow \text{length} = 2r$
This length is said to be the displacement of the particle. We already know the time interval given to be ${t_0}$ and hence the values are substituted in the equation ($2$). We get:
$v = \dfrac{{2r}}{{{t_0}}}$
Thus, the average velocity of the particle which travels half the circle has a magnitude equivalent to $\dfrac{{2r}}{{{t_0}}}$. Hence, the average speed of the particle is $\dfrac{{\pi r}}{{{t_0}}}$ and the average velocity of the particle is $\dfrac{{2r}}{{{t_0}}}$.

Therefore, the correct option is option C.

Additional information: The two quantities displacement and the distance are said to have major differences. Since distance is a scalar quantity the distance value is always said to be zero or positive but displacement can have negative values as well. The displacement is independent of the path traversed by the particle. It only depends on the initial and the final values of the particle or in other words it is said to consider only the source and destination points and tends to consider the shortest route.

The magnitude of average velocity and average speeds are said to be equal at certain conditions. This occurs when the path taken for both distance and displacement is the same.This happens when an object travels along a straight line of motion and must be in the same direction, then distance of the path length will be equivalent to the magnitude of displacement.Even-though velocity and speed are different concept wise they have the same dimensional formula. The dimensional formula for speed or velocity is given to be: $\left[ {{M^0}L{T^{ - 1}}} \right]$

Note: The two quantities, namely, speed and velocity are two differing concepts and are often mistaken to be the same where speed depends on the distance covered and one depends on the displacement which also seem to be two different quantities. There is another misconception that when considering only the magnitudes of these quantities then both their values are the same since velocity is a vector quantity and here the direction is not taken into consideration; which is wrong. This is clear from the above example that the speeds and velocities of the same particle are different in magnitudes.