Question

A point source of light is kept below the surface of water (${{n}_{w}}$​=4/3) at a depth of $\sqrt{7}$m. The radius of the circular bright patch of light noticed on the surface of water is ______ m

A. $\dfrac{3}{\sqrt{7}}$
B. $3$
C. $\dfrac{\sqrt{7}}{3}$
D. $\sqrt{7}$

Answer 1

Hint: Here, the light escapes from water to the outer air by the principle of refraction. Water is the denser medium and air is the rarer medium. The ray of light comes out along the surface, hence the angle of refraction is the critical angle.

Formula Used:
If the critical angle is C, then $\sin C=\dfrac{1}{n}$, where n is the refractive index of the material.

Complete step by step answer:

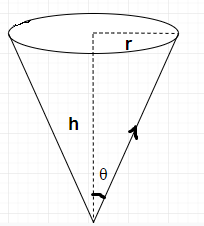
Let us consider the radius of the circular patch be $r$
The light rays graze along the surface of the water body. Hence, the angle of refraction is ${{90}^{\circ }}$. Therefore we can say that $\theta $is the critical angle, that is the angle of incidence when the angle of refraction is ${{90}^{\circ }}$
We are given that the value of $h$ is $\sqrt{7}m$, and the refractive index of water \[{{n}_{w}}\]is 4/3
Since $\theta $is the critical angle, we can say that
  $\begin{align}
  & \sin \theta =\dfrac{1}{{{n}_{w}}} \\
 & \therefore \sin \theta =\dfrac{3}{4} \\
\end{align}$
We know that
 $\begin{align}
  & {{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \\
 & \Rightarrow \cos \theta =\sqrt{1-{{\sin }^{2}}\theta }=\sqrt{1-{{(\dfrac{3}{4})}^{2}}}=\dfrac{\sqrt{7}}{4} \\
\end{align}$
Hence, \[\tan \theta =\dfrac{\sin \theta }{\cos \theta }=\dfrac{3}{\sqrt{7}}\]
But from figure, we can infer that $\tan \theta =\dfrac{r}{h}$
$\begin{align}
  & \Rightarrow \dfrac{r}{\sqrt{7}}=\dfrac{3}{\sqrt{7}} \\
 & \therefore r=3 \\
\end{align}$
Therefore, the radius of the circular bright patch of light noticed on the surface of water is 3 m
We can conclude that option B is the correct answer among the given options.

Note:When students are given such questions, they are expected to diagrammatically represent the given situation. This would make it easier to deduce the answer geometrically and also, this is an impressive way of presenting the answer for the exams.