Question

A point source of light is hung 30 feet directly above a straight horizontal path on which a man of 6 feet in height is walking. How fast is the man’s shadow lengthening and how fast the tip of the shadow is moving when he is walking away from the light at the rate of 100ft/min.

Answer 1

Hint: Two objects are similar if they have the same shape, they can have different sizes and orientations. There are several ways to prove two triangles similar, some of them are AA similarity criterion, SAS similarity criterion, and SSS similarity criterion. Use a suitable way to prove the two triangles similar and find out the relation between x and y to obtain the correct answer.

Complete step-by-step answer:

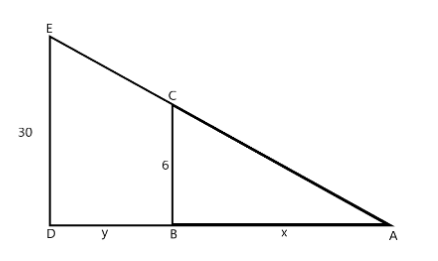
In the figure, E is the point source of light hung 30 feet directly above the straight horizontal path. CD represents the man of height 6 feet. As the light source is directly above the ground, it makes an angle of $90^\circ $ with the horizontal path and a man also walks perpendicularly on the horizontal surface. So $\angle CBA = \angle EDA = 90^\circ $
Also, $\angle CAB = \angle EAD$ as it is common in both the triangles.
So, by AA similarity criterion $\vartriangle CBA \sim \vartriangle EDA$
As the two triangles are similar, so $\dfrac{{CB}}{{ED}} = \dfrac{{BA}}{{DA}} = \dfrac{{CA}}{{EA}}$
$
\Rightarrow \dfrac{{CB}}{{ED}} = \dfrac{{BA}}{{EA}} \\
\Rightarrow \dfrac{6}{{30}} = \dfrac{x}{{x + y}} \\
\Rightarrow 6x + 6y = 30x \\
\Rightarrow 6y = 24x \\
\Rightarrow y = 4x \;
 $
Now, we know that the man is walking at the speed of 100 ft/min so $\dfrac{{dx}}{{dt}} = 100\;ft\min $
Differentiating both sides of the obtained equation with respect to time, we get –
$
  4(\dfrac{{dy}}{{dt}}) = \dfrac{{dx}}{{dt}} \\
  4(\dfrac{{dy}}{{dt}}) = 100 \\
  \dfrac{{dy}}{{dt}} = 25\;ft/\min \;
 $
Thus, man’s shadow is lengthening at the rate of 25 ft/min.
$
  DA = DB + BA \\
  DA = x + y \;
 $
Let the length of DA be z,
$z = x + y$
Differentiate both sides with respect to the time.
$
  \dfrac{{dz}}{{dt}} = \dfrac{{dx}}{{dt}} + \dfrac{{dy}}{{dt}} \\
  \dfrac{{dz}}{{dt}} = 100 + 25 \\
  \dfrac{{dz}}{{dt}} = 125\;ft/\min \;
 $
Therefore, the tip of the shadow is moving at a speed of 125 ft/min.
So, the correct answer is “125 ft/min”.

Note: If any two or more angles of a triangle are equal to any two or more angles of another triangle, then the two triangles are said to be similar. The instantaneous rate of change of a function with respect to a variable is called derivative or differentiation. In this question time is the variable.