Question

A point source has been placed as shown in the figure. What is the length on the screen that will receive reflected light from the mirror?

A) $2H$
B) $3H$
C) $H$
D) None of the above

Answer 1

Hint: The question is from Ray optics and the concept of reflection of light is used. The question is solved by using laws of reflection of light and congruent triangles property. Also according to laws of reflection, the angle of incidence is the same as that of angle of reflection.

Complete step by step answer:
In the question a point source ‘S’ is placed at height ‘H’ from the ground. A screen is placed at the other side. The light reflects from the mirror and reflects on the screen at 2 points. We have to find the length on the screen that will receive reflected light from the mirror as shown below:

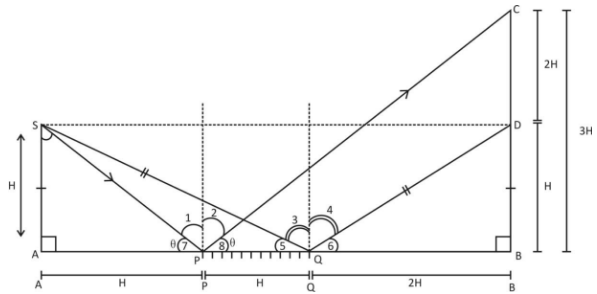
As reflection is the bouncing back of light in the same medium when it falls on some reflecting surface. Angle of incidence is the angle which the incident ray makes with the normal and the angle of reflection is the angle which the reflected ray makes with the normal.
As we know that by laws of reflection, we have
The angle of incidence $ = $ angle of reflection
So, $\angle 1 = \angle 2$
$\angle 3 = \angle 4$
Also, \[\angle 5 = \angle 6\] (vertically opposite angle)
Now in,
$\Delta ASQ\,\;and\;\,\Delta QDB; \\
\Rightarrow \angle 5 = \angle 6 \left( {vertically{\text{ }}opposite{\text{ }}angel} \right) \\
\Rightarrow \angle SAQ = \angle DBQ (90^\circ ) \\
\Rightarrow AQ = QB ( = 2H) \\
$
Hence, $\Delta 's$ are congruent by ASA congruence
So the lengths AS and DB will also be equal. This is by CPCT that is congruent parts of congruent triangles. So, \[AS = DB = H\]
Now, \[\angle 7 = \angle 8 = \theta \] (vertically opposite angle)
In $\Delta SAP$
$
tan\theta = \dfrac{{AS}}{{AP}} = \dfrac{H}{H} = 1 \\
\Rightarrow tan\,\theta = 1 \\
\Rightarrow \theta = 45^\circ \\ $
So, we can have $\angle 7 = \angle 8 = 45^\circ $
So, in $\Delta PCB$
$
tan\theta = \dfrac{{BC}}{{PB}} \\
\Rightarrow 1 = \dfrac{{BC}}{{3H}} \\
\therefore \;BC = 3H \\
 $
Hence, length of screen $CD = BC - BD$
$CD = 3H - H$
$CD = 2H$
So, the length of the screen is 2H.

So, the correct answer is Option (A).

Note: $\angle i = \angle r,$ for reflection to take place, also to find the length of screen, subtract BD from BC. This is because the length of screen is only the CD part shown in the figure. When two triangles are congruent, this means that corresponding sides and angles will also be equal.