Question

A point $ P\left( \sqrt{3},1 \right) $ moves on the circle $ {{x}^{2}}+{{y}^{2}}=4 $ . After covering a quarter of the circle, it leaves the circle tangentially. The equation of line along which the point moves after leaving the circle is
(a) $ y=\sqrt{3}x+4 $
(b) $ \sqrt{3}y=x+4 $
(c) $ \sqrt{3}y=x-4 $
(d) $ y=\sqrt{3}x-4 $

Answer 1

Hint: First, we will draw the circle as per given data. We will get as

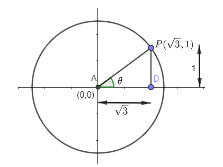
Then we will find angle $ \theta $ using the formula $ \tan \theta =\dfrac{opposite}{adjacent} $ . Then it is told that point moves to the quarter of the circle and leaves tangentially. So, it means that from point P till 90 degree we will mark point I in anticlockwise direction and in clockwise direction to point J. Then using the formula to find coordinate $ \left( r\cos \theta ,r\sin \theta \right) $ we will get points I and J. Then, we will use equation to find tangent which is given as $ x{{x}_{1}}+y{{y}_{1}}={{r}^{2}} $ where $ \left( {{x}_{1}},{{y}_{1}} \right) $ are coordinates at particular point. Thus, on solving for point I and J, we will get two options correct.

Complete step-by-step answer:
Then we will find angle $ \theta $ using the formula $ \tan \theta =\dfrac{opposite}{adjacent} $ . Then it is told that point moves to the quarter of the circle and leaves tangentially. So, it means that from point P till 90 degree we will mark point I in anticlockwise direction and in clockwise direction to point J. Then using the formula to find coordinate $ \left( r\cos \theta ,r\sin \theta \right) $ we will get points I and J. Then, we will use equation to find tangent which is given as $ x{{x}_{1}}+y{{y}_{1}}={{r}^{2}} $ where $ \left( {{x}_{1}},{{y}_{1}} \right) $ are coordinates at particular point. Thus, on solving for point I and J, we will get two options correct.

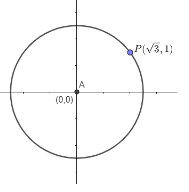
Here, first we will draw a circle and will plot the point $ P\left( \sqrt{3},1 \right) $ approximately. We get as

Now, we will join the centre point with point P. So, we will get a triangle with some angle $ \theta $ .

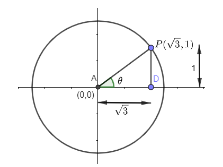
So, from this we get the value of angle using the trigonometric rule $ \tan \theta =\dfrac{opposite}{adjacent} $ . By applying this rule, we get as
 $ \tan \theta =\dfrac{opposite}{adjacent}=\dfrac{PD}{AD} $
 $ \tan \theta =\dfrac{1}{\sqrt{3}} $
We know that $ \tan 30{}^\circ =\dfrac{1}{\sqrt{3}} $ . So, $ \theta =30{}^\circ $ which in radian form can be written as $ \theta =30{}^\circ \times \dfrac{\pi }{180{}^\circ }=\dfrac{\pi }{6} $ .
Now, it is given that the point covers the quarter circle and leaves the circle tangentially. It means that the circle has a total angle of 360. Quarter means $ \dfrac{1}{4} $ so, we get an angle as $ \dfrac{1}{4}\times 360=90{}^\circ $ . So, point moves $ 90{}^\circ $ in clockwise or anticlockwise direction. In radian form $ 90{}^\circ $ is $ \dfrac{\pi }{2} $ . Figure is as shown below.

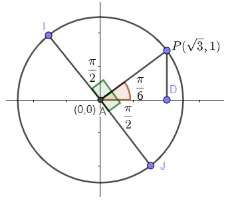
So, now total angle till point I from centre is $ \dfrac{\pi }{6}+\dfrac{\pi }{2}=\dfrac{4\pi }{6}\Rightarrow \dfrac{2\pi }{3} $ and total angle from centre till point J is $ \dfrac{\pi }{6}-\dfrac{\pi }{2}=\dfrac{-2\pi }{6}\Rightarrow -\dfrac{\pi }{3} $ .
So, coordinates of point I and J i.e. tangent can be found out using the formula $ \left( r\cos \theta ,r\sin \theta \right) $ where the radius of the circle. So, we can find out from circle equation $ {{x}^{2}}+{{y}^{2}}=4 $ which is in form $ {{x}^{2}}+{{y}^{2}}={{r}^{2}} $ . So, from this we will get $ r=2 $ .
Thus, coordinates of point I is $ \left( 2\cos \dfrac{2\pi }{3},2\sin \dfrac{2\pi }{3} \right) $ and for J is $ \left( 2\cos \dfrac{-\pi }{3},2\sin \dfrac{-\pi }{3} \right) $ .
Value of $ \dfrac{2\pi }{3}=\pi -\dfrac{\pi }{3} $ . So, we can say that $ \cos \dfrac{\pi }{3}=\dfrac{1}{2} $ and $ \sin \dfrac{\pi }{3}=\dfrac{\sqrt{3}}{2} $ . As the tangent is in second quadrant, cos value will be negative and sin value will be positive.
Thus, on substituting the values and solving we get as $ I\left( -1,\sqrt{3} \right) $ .
Similarly, for point J we get as $ J\left( 1,-\sqrt{3} \right) $ .
Now, to find equation of tangent at a point formula will be $ x{{x}_{1}}+y{{y}_{1}}={{r}^{2}} $ where $ \left( {{x}_{1}},{{y}_{1}} \right) $ are coordinates at particular point.
So, tangent t point I will be
 $ x\left( -1 \right)+y\left( \sqrt{3} \right)={{2}^{2}} $
 $ -x+\sqrt{3}y=4 $
 $ \Rightarrow \sqrt{3}y=x+4 $ …………………(1)
Similarly, for point J we get as
 $ x\left( 1 \right)+y\left( -\sqrt{3} \right)={{2}^{2}} $
\[x-\sqrt{3}y=4\]
\[\Rightarrow x-4=\sqrt{3}y\] ………………………(2)
Thus, option (b) and (c) is correct.

Note: In this type of diagram figure is very necessary. If solved without a figure, there are chances of getting an incorrect answer. Students should know the formula to find coordinates points using the formula $ \left( r\cos \theta ,r\sin \theta \right) $ . Also, students take radius of circle 4 instead of 2 and due to this silly mistake the whole answer will be wrong. So, be careful while solving it.