Question

A point object O is placed on the principal axis of a convex lens of focal length f= 20cm at a distance of 40cm to the left of it. The diameter of the lens is 10cm. An eye is placed 60cm to the right of the lens and a distance h below the principal axis. The maximum value of h to see the image is
A. Zero
B. 2.5cm
C. 5cm
D. 10cm

Answer 1

Hint: This type of optics questions always utilize the lens formula. Here we can calculate image distance using this formula. Then simple mathematical symmetry of triangles aids us in calculating the value of h.
Formula Used: Lens Formula:
$$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$$
Where f is the focal length of lens, v is the distance of image from lens and u is the distance of object from lens.

Complete Step-by-Step solution:
While solving optics questions like this, lens formulas always come handy. We have the following values given to us.
f=20cm
u=-40cm
Solving for v using lens formula, we get
$
 \dfrac{1}{{20}} = \dfrac{1}{v} - \dfrac{1}{{( - 40)}} \\
   \Rightarrow \dfrac{1}{{20}} = \dfrac{1}{v} + \dfrac{1}{{40}} \\
   \Rightarrow \dfrac{1}{v} = \dfrac{1}{{20}} - \dfrac{1}{{40}} \\
   \Rightarrow \dfrac{1}{v} = \dfrac{{2 - 1}}{{40}} \\
   \Rightarrow \dfrac{1}{v} = \dfrac{1}{{40}} \\
   \Rightarrow v = 40cm \\
 $
This means that the image is formed at the center of curvature. Therefore, we can draw the ray diagram as follows.

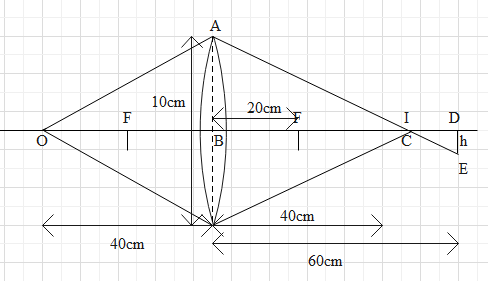
Now in the figure, $\Delta$CED and $\Delta$CAB are symmetric. So we have
$ \dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{DC}} \\
   \Rightarrow \dfrac{5}{h} = \dfrac{{40}}{{20}} \\
   \Rightarrow \dfrac{5}{h} = 2 \\
   \Rightarrow h = \dfrac{5}{2} \\
   \Rightarrow h = 2.5cm \\ $
This is the required answer. Hence, the correct option is option B.
Additional Information:
We can also calculate the magnification of an object using the following formula.
$$M = \dfrac{{{h_i}}}{{{h_o}}} = - \dfrac{v}{u}$$
where $h_i$ is the height of the image and $h_o$ is the height of the object.

Note: The student must take care of the convention followed for the signs of various distances. Take care of the negative sign for u and positive sign for v. All distances to the left of the lens are taken as negative whereas all the distances to the right of the lens are taken as positive.