Question

 A point is such that the perpendicular from the centre on its polar with respect to the ellipse and equal to c; Show that its locus is the ellipse
\[\dfrac{{{x}^{2}}}{{{a}^{4}}}+\dfrac{{{y}^{2}}}{{{b}^{4}}}=\dfrac{1}{{{c}^{2}}}\]

Answer 1

Hint: Write the equation of polar w.r.t pole and calculate perpendicular distance of it from centre and use the given condition.

Complete step-by-step answer:
Let us consider equation of ellipse
\[\dfrac{{{x}^{2}}}{{{a}^{4}}}+\dfrac{{{y}^{2}}}{{{b}^{4}}}=\dfrac{1}{{{c}^{2}}}\] (\[\because \]a > b) (Assumption)

As we know that polar is the w.r.t pole in ellipse in a way like: -
As there are infinite numbers of lines can be drawn through P and each can be termed as chord and cut at two points to ellipse. Tangents (two) can be drawn through each chord and ellipse intersection point as shown below: -

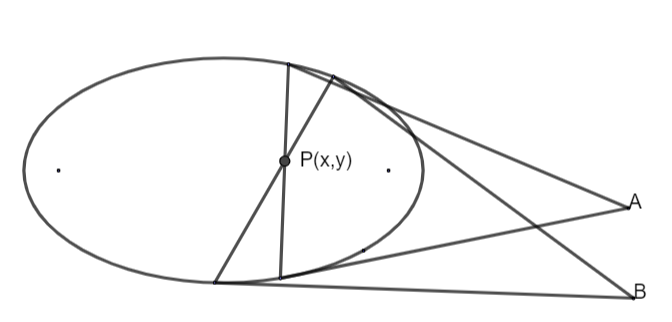
Line joining the points A and B will be termed as polar i.e. all the points we get after drawing two tangents w.r.t P(pole) will lie on a line which is called polar and the equation of that line is T=0.

i.e. \[\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1\]

Now, coming to the question
Equation of ellipse\[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]
Pole assumed= P (h, k)
Polar w.r.t pole \[\Rightarrow T=0\]
\[\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1\]-(2)

Perpendicular distance from centre (0,0) to polar i.e.
\[\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1\]

Perpendicular distance = \[\left| \dfrac{\dfrac{h}{{{a}^{2}}}\left( 0 \right)+\dfrac{k}{{{b}^{2}}}\left( 0 \right)-1}{\sqrt{{{\left( \dfrac{h}{{{a}^{2}}} \right)}^{2}}+{{\left( \dfrac{k}{{{b}^{2}}} \right)}^{2}}}} \right|\]
(\[\because \]As we know that perpendicular distance from any point \[\left( {{x}_{1}},{{y}_{1}} \right)\] to any line \[ax+by+c=0\] is \[\left| \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|\])

We have given that perpendicular distance is c from the centre to the polar of the ellipse.
\[c=\left| \dfrac{-1}{\sqrt{\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}}} \right|\]

Squaring both sides of the equation
\[\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}=\dfrac{1}{{{c}^{2}}}\]

Replacing (h, k) to (x, y) to get locus.
\[\dfrac{{{x}^{2}}}{{{a}^{4}}}+\dfrac{{{y}^{2}}}{{{b}^{4}}}=\dfrac{1}{{{c}^{2}}}\]
Hence, proved.

Note: One need to clear about the concepts of pole and polar. Direct equation of polar with respect to any pole is T=0 i.e. If standard equation of ellipse is \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]and (h, k) is a pole then polar can be written as \[\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1\].
We need to assume standard equations to prove these kinds of questions always to keep the flexibility of the solution.