Question

A plate of mass m, length b and breadth a is initially lying on a horizontal floor with length parallel to the floor and breadth perpendicular to the floor. The work done to erect it on its breadth is
(A). \[mg\left[ \dfrac{b}{2} \right]\]
(B). \[mg\left[ a+\dfrac{b}{2} \right]\]
(C). \[mg\left[ \dfrac{b-a}{2} \right]\]
(D). \[mg\left[ \dfrac{b+a}{2} \right]\]

Answer 1

Hint: We can find out this work done by calculating the potential energy of each case. Potential energy is the energy possessed by its state of position. The energy stored in an object as the result of its height is known as the gravitational potential energy. The work done can be written as the change in gravitational potential energy.

Complete step by step answer:

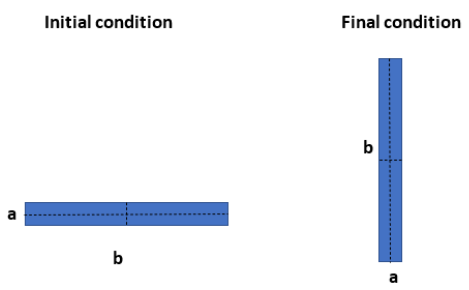
Here we are considering a plate of mass m. Initially, it is lying on the floor with its length side like the figure shown above. In the final case, the plate is lying on its breadth side like the figure shown above. We can find the work done for the transformation of orientation. As we know, if there is a change in gravitational potential energy then there will be work done. So, we can find out the potential energy of the body in each case.
In the first case, the plate is lying on the length side. So, the breadth side will be the height. Since it is a well-shaped and uniform structure its centre of gravity will be at \[\dfrac{a}{2}\]. So we can take this as the height.
\[{{h}_{1}}=\dfrac{a}{2}\]
So the gravitational potential energy will be,
\[mg{{h}_{1}}=mg\dfrac{a}{2}\], where m is the mass of the object, g is the acceleration due to gravity, a is the breadth of the plate.
In the second case, the plate is lying with the breadth side of the plate. Since it is well-shaped and uniform, the centre of gravity will be at \[\dfrac{b}{2}\]. So we can take this as height.
\[{{h}_{2}}=\dfrac{b}{2}\]
Hence, the gravitational potential energy of the second case will be,
\[mg{{h}_{2}}=mg\dfrac{b}{2}\]
\[\text{Work done = change in gravitational potential energy}\]
\[W=mg{{h}_{2}}-mg{{h}_{1}}\]
Since mass and acceleration due to gravity are the same in both cases, we can take it outside.
\[W=mg({{h}_{2}}-{{h}_{1}})\]
Now we can assign the heights in respective places.
\[W=mg\left( \dfrac{b}{2}-\dfrac{a}{2} \right)=mg\left( \dfrac{b-a}{2} \right)\]
So the correct option is C.

Note: We can do this problem by finding the height difference and then by multiplying with force. In this case, the force will be weight. Here we are considering heights of the centre of gravity of the plate, not the actual heights. We are not applying any other forces here and the object is uniformly distributed and well-shaped structure. So we can simply say about the centre of gravity of that object more than any other point.