Question

A plastic box $1.5m$ long, $1.25m$ wide and $65cm$ deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet, determine:
(i) The area of the sheet required for making the box
(ii) The cost of the sheet for it, if a sheet measuring $1{m^2}$costs $Rs20$

Answer 1

Hint: Imagine the box being a cuboid with all the faces except the top. And the top itself is just a rectangular face with dimensions the same as the bottom base.

Complete step by step answer:

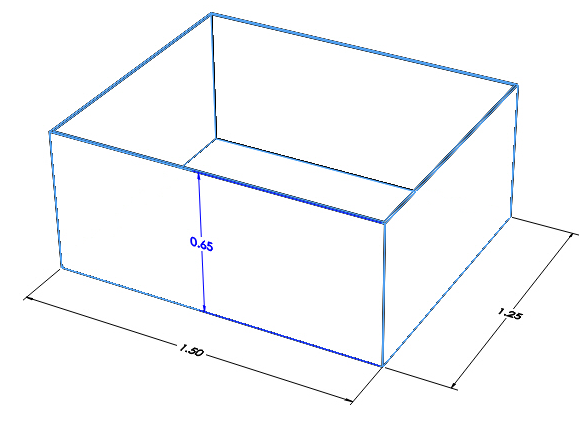
Given data in question is that length$\left( l \right)$ is $1.5m$, breath$\left( b \right)$ is $1.25m$ and depth$\left( h \right)$is $65cm = \dfrac{{65}}{{100}}m = 0.65m$
And the box is opened from the top, i.e. the box is in the form of Cuboid with$4$faces on sides and one on base.
So to calculate the area of the sheet required for making the box all we need to do is to calculate the area of $4$ rectangular side faces and $1$ rectangular base at the bottom.
As we know, the total surface area of a Cuboid$ = 2 \times \left( {lb + bh + hl} \right)$
But the top area should not be included in this according to the question. Since the top area $ = l \times b$
Therefore,
Area of sheets required$ = 2 \times \left( {lb + bh + hl} \right) - lb = lb + 2 \times \left( {bh + hl} \right)$
Let’s substitute the given values in our formula
Area of sheets\[ = (1.5 \times 1.25) + 2 \times \left[ {\left( {1.25 \times 0.65} \right) + \left( {0.65 \times 1.5} \right)} \right]\]
Solving multiplication inside braces first, we see
Area of sheets\[ = (1.875) + 2 \times \left[ {\left( {0.8125} \right) + \left( {0.975} \right)} \right] = 1.875 + 2 \times (1.7875) = 1.875 + 3.575\]
Hence,
Area of sheets$ = 5.45{m^2}$
Now according to (ii), the cost of the sheet needs to be calculated.
Given that the cost of $1{m^2}$ the area of the sheet is $Rs20$, i.e. the rate of the sheet is $Rs20$per $1{m^2}$of area.
Total cost$ = $ Area of sheets $ \times $Rate of buying sheet
Total Cost of sheets required for the box is $Rs$$ = 5.45 \times 20 = 109$

$\therefore $Total Cost of sheets required for the box is Rs.109

Note:
In Mensuration, never forget to notice the units of all the given data. Always convert the units in the same format before starting the solution. Be careful while removing the top area and use braces to avoid any chances of getting confused. Another approach to this problem is that you can use the formula for the area of four walls of the box and then add the area of bottom in it. This will eventually give the same above relation, i.e. Area of sheets required$ = lb + 2 \times \left( {bh + hl} \right)$.