Question

A plank with a box on it at one end is gradually raised about the other end. As the angle of inclination with the horizontal reaches ${{30}^{o}}$, the box starts to slip and slides 4.0m down the plank in 4.0s. The coefficients of static and kinetic friction between the box and the plank will be, respectively.

A. 0.4 and 0.3
B. 0.6 and 0.6
C. 0.6 and 0.5
D. 0.5 and 0.6

Answer 1

Hint: In this question we have been provided with two cases one where box was just about to slip and box started to slip. In the first case use the concept of angle of repose where tangent of angle is equal to static friction. In the second case, mg acts downwards whereas normal acts perpendicular. Resolve components of mg. write force equation, put values in that equation and calculate value of coefficient kinetic friction.
Formula used:
$\tan \theta ={{\mu }_{s}}$
Where, θ = angle between plane surface and inclination
${{\mu }_{s}}$= coefficient of static friction.

Complete answer:
A plank with a box on it is shown in figure below

This is the initial condition.
Consider Now raised the plank in the direction of the arrow from one end by one end at fix. Plank is raised by an angle${{30}^{o}}$. Therefore the figure will looks like

It is given that when θ reaches at ${{30}^{o}}$ a box starts slipping in downwards direction. Therefore θ = ${{30}^{o}}$ is the angle of repose. Angle of repose is nothing but the minimum angle from where the body starts to slip. We know that the tangent of angle of repose is equal to the static friction.
$\begin{align}
  & \therefore \tan \theta ={{\mu }_{s}} \\
 & \therefore {{\mu }_{s}}=\tan {{30}^{o}} \\
 & \therefore {{\mu }_{s}}=\dfrac{1}{\sqrt{3}}\approx 0.6 \\
\end{align}$
Hence static friction is 0.67 now next condition is the box is slipping and it covers distance 4m in 4s seconds it means starting velocity of box is zero i.e. u = 0, s = 4m, t = 4s
Apply kinematic equation,
$\begin{align}
  & \therefore s=ut+\dfrac{1}{2}a{{t}^{2}} \\
 & \Rightarrow 4=0+\dfrac{1}{2}a{{4}^{2}} \\
 & \Rightarrow 4=\dfrac{1}{2}16a \\
 & \Rightarrow \dfrac{4}{8}=a \\
 & \therefore a=\dfrac{1}{2}\Rightarrow 0.5 \\
\end{align}$
So $0.5m/{{s}^{2}}$ is the acceleration of the box with which box started slipping.
Now let’s draw the diagram to resolve the forces,

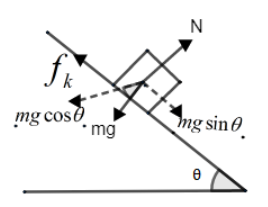
As we can say in figure mg is acting downwards and normal (N) is acting perpendicular to the box. Now resolve components of mg into sine and cosine as $mg\sin \theta \text{ and }mg\cos \theta $ respectively. Here we have taken $mg\cos \theta $ in left of mg, not right side of mg because we know that a component of cosine has always taken in the direction of θ or angle or towards the angle as shown in the figure.
Since box is slipping therefore kinetic friction which act opposite to the direction of $mg\sin \theta $ which is given by,
${{f}_{k}}={{\mu }_{u}}N.......(1)$
Therefore write force equation we have,
$mg\sin \theta =ma+{{f}_{k}}........(2)$
$N=mg\cos \theta $ (Since normal is balancing cosine components of mg)
Therefore equation (1) implies
${{f}_{k}}={{\mu }_{k}}mg\cos \theta $
Therefore equation (2) implies
$\begin{align}
  & mg\sin \theta -{{\mu }_{k}}mg\cos \theta =ma \\
 & \Rightarrow {{\mu }_{k}}=\dfrac{g\sin \theta -a}{g\cos \theta } \\
\end{align}$
Put values we get,
$\begin{align}
  & {{\mu }_{k}}=\dfrac{10\times \sin {{30}^{o}}-0.5}{10\times \dfrac{\sqrt{3}}{2}} \\
 & {{\mu }_{k}}=\left( \dfrac{10}{2}-\left( \dfrac{1}{2} \right) \right)\dfrac{2}{10\sqrt{3}} \\
 & {{\mu }_{k}}=0.5 \\
\end{align}$
Hence coefficient of static friction and kinetic friction between the box and the plank will be 0.6 and 0.5 respectively.

Correct Option is C.

Note:
The process of raising one edge over another i.e. keeping another edge fixed through a certain angle is known as banking of objects. So here, in this question we have used the concepts of banking of objects. The angle made by the surface of the plank with the horizontal surface is called angle of banking.