Question

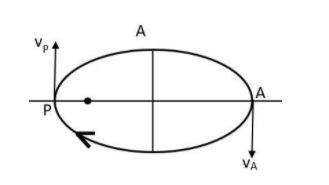
A planet orbits in an elliptical path of eccentricity $e$ around a massive star considered fixed at one of the foci. The point in space where it is closest to the star is denoted by P and the point where it is farthest is denoted by A. Let ${v}_{P}$ and ${v}_{A}$ be the respective speeds at P and A. Then

(a). $\dfrac{{V}_{P}}{{V}_{A}}=\dfrac{1+e}{1-e}$
(b). $\dfrac{{V}_{P}}{{V}_{A}}=1$
(c). $\dfrac{{V}_{P}}{{V}_{A}}=\dfrac{1+e^2}{1-e}$
(d). $\dfrac{{V}_{P}}{{V}_{A}}=\dfrac{1+e^2}{1-e^2}$

Answer 1

Hint: Here, the planet is revolving around the star, so at both points A and P, the masses will be the same. Thus, we can apply here the conservation of angular momentum concept to determine the ratio of velocities. The angular momentum can be found out by using the formula $\vec{L}=\vec{r}\times (m\vec{v})=mvrsin\theta$, where, r is the distance, m is the mass and v is the speed of the object and $\theta$ is the angle displacement vector makes with the velocity vector.

Complete step by step solution:
We have been given that the planet is orbiting around the star located at one of the foci. Also, P and A are points closest and farthest to it respectively.
Let the distance between the star and the points P and A are ${r}_{P}$ and ${r}_{A}$ respectively. And we can also see that the velocity vector is perpendicular to the displacement vector.
So, we will now find the angular momentum of the planet at point A and P using the formula $\vec{L}=\vec{r}\times (m\vec{v})=mvrsin\theta$, where, r is the distance, m is the mass and v is the speed of the object and $\theta$ is the angle displacement vector makes with the velocity vector.
At point P, the angular momentum of the planet, ${{L}_{P}}=m{v}_{P}{r}_{P}sin90^\circ= m{v}_{P}{r}_{P}$
And similarly, at point A, the angular momentum will be ${L}_{A}= m{v}_{A}{r}_{A}$
On applying conservation of angular momentum for points P and A, we will have, ${L}_{P}={L}_{A}\implies m{v}_{P}{r}_{P}= m{v}_{A}{r}_{A}\implies \dfrac{{V}_{P}}{{V}_{A}}=\dfrac{{r}_{A}}{{r}_{P}}$.......... (i)
Now, let us assume the length of the semi major axis of the elliptical orbit is $a$. And we also know that the semi major axis of an ellipse is the mean value of the minimum and maximum distances of the ellipse from a focus. And here, ${r}_{P}$ and ${r}_{A}$ are respectively the minimum and maximum distance from the star located at the foci.
Thus, we can write ${r}_{P}=a(1-e)$ and ${r}_{A}=a(1+e)$. Putting this in equation (i), we get
$\dfrac{{V}_{P}}{{V}_{A}}=\dfrac{{r}_{A}}{{r}_{P}}=\dfrac{a(1+e)}{a(1-e)}$
$\implies \dfrac{{V}_{P}}{{V}_{A}}=\dfrac{1+e}{1-e}$
Hence, option a is the correct answer.

Note: To solve this question, we can also use Kepler’s law which describes the motion of planets around the sun. It states that a line segment joining the sun and a planet sweeps out equal area in equal intervals of time. Although, the approach of angular velocity is easier and simpler in respect to the Kepler’s law approach.