Question

A plane sound wave is traveling in a medium. In reference to frame A, its equation is \[y = a\cos \left( {\omega t - kx} \right)\]. Which to a frame B, moving with a constant velocity v in the direction of propagation of the wave, equation of the wave will be: -

A. \[y = a\cos \left[ {\left( {\omega t + kv} \right)t - kx} \right]\]
B. \[y = - a\cos \left[ {\left( {\omega t - kv} \right)t - kx} \right]\]
C. \[y = a\cos \left[ {\left( {\omega t - kv} \right)t - kx} \right]\]
D. \[y = a\cos \left[ {\left( {\omega t - kv} \right)t + kx} \right]\]

Answer 1

Hint: In this question equation of a wave is given now; it is being said that another frame which is in motion with a velocity v, so we need to find the changes in the wave equation due to the movement of the frame.

Complete step by step answer:
Given the velocity of the wave with reference to the frame A where the frame is constant, is given as
\[y = a\cos \left( {\omega t - kx} \right) - - (i)\]

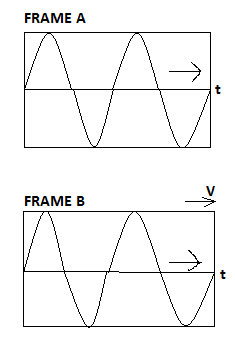
Now for frame B here, the frame is also moving with the sound wave in the direction of propagation with a velocity v.
Here the wave and the frame both are moving in the same direction, so if we observe a point in the wave at time t, we get
 \[x' = x - vt - - (ii)\]
Now, if we observe the wave moving with velocity v with frame A, we can write equation (ii) as
\[x = x' + vt - - (iii)\]
Now to find the equation of the wave for frame B, substitute equation (iii) in equation (i) to get the wave equation
 \[
  y = a\cos \left( {\omega t - k\left( {x' + vt} \right)} \right) \\
   = a\cos \left( {\left( {\omega - kv} \right)t - kx'} \right) \\
   = a\cos \left( {\omega t - kvt - kx'} \right) \\
 \]
Hence the equation of the wave in reference to frame B is
\[y = a\cos \left( {\omega t - kvt - kx'} \right)\]
Option (C) is correct.

Note:Students must note that when a particle and the reference are both moving in the same direction, then the relative velocity between them decreases, but when they are moving in a different direction, then the relative speed increases.