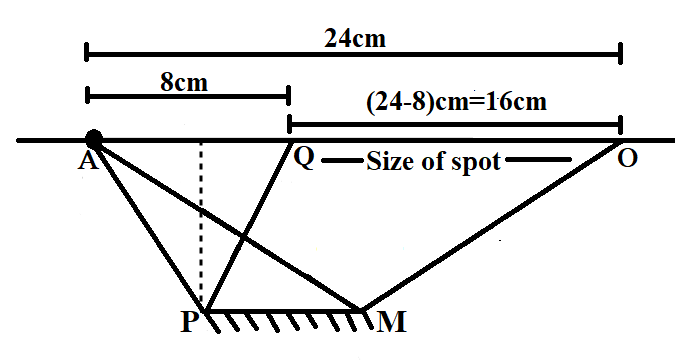
A plane mirror of length $8cm$ is moving with speed $3m{{s}^{-1}}$ towards a wall in the situation as shown in the figure. Size of the spot formed on the wall is $\dfrac{32}{x}cm$. Find the value of $x$.
Answer
Verified571.8k+ views
Hint: When light falls on a plane mirror, the light gets reflected. Reflection from a plane mirror is in such a way that the angle of incidence is equal to the angle of reflection. From the property of equality of angles in triangles, opposite sides subtended by equal angles of triangles will have equal lengths. Size of the spot is calculated using this principle and is finally equated to $\dfrac{32}{x}cm$, to get the value of $x$.
Complete answer:
We are given that a plane mirror of length $8cm$ is moving with speed $3m{{s}^{-1}}$ towards a wall in the situation as shown in the following figure.
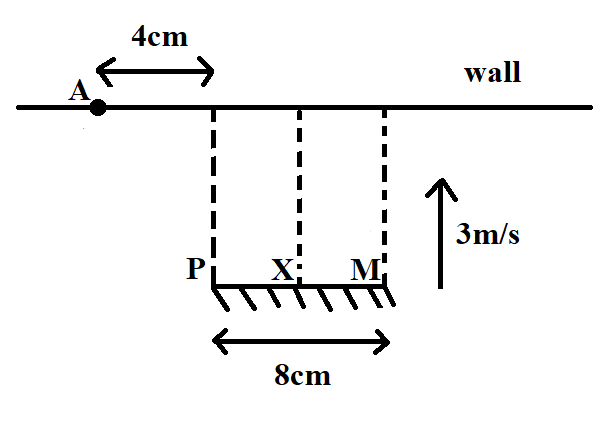
Clearly, the distance of the light source from the wall is $4cm$. We are required to find the size of the spot, projected on the wall, after reflection from the plane mirror.
According to the laws of reflection, the angle of incidence is equal to the angle of reflection. Angle of incidence is nothing but the angle between the incident ray of light source and the perpendicular tangent drawn at the point of incidence on the plane mirror. Similarly, angle of reflection is nothing but the angle between the reflected ray and the perpendicular tangent drawn at the point of reflection. Clearly, point of incidence is equal to point of reflection.
We also know that if two angles of two different triangles are equal, both these angles will subtend equal lengths on the opposite sides of these triangles.
Now, let us apply the law of reflection and the property of equal angles in triangles to each incident ray and its corresponding reflected ray. We consider three points of reflection-the first one being the extreme left point of the plane mirror, the second one being the midpoint of the plane mirror and the third one being the extreme right point of the plane mirror. Clearly, these points are $P,X$ and $M$, respectively, as can be seen from the figure given above.
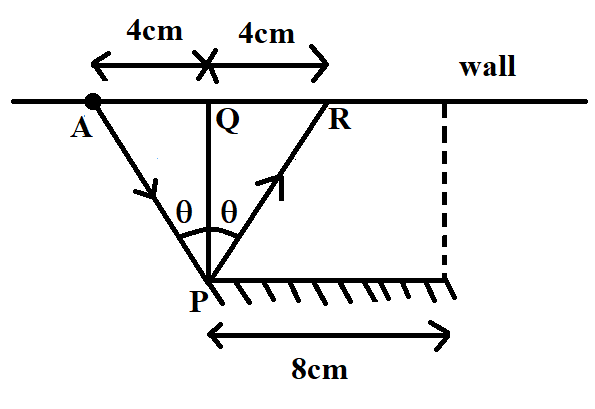
Let us take the case of reflection from point $P$. The incident ray coming from the light source gets reflected and forms a spot on the wall at a distance of $4cm$ from the extended perpendicular tangent, drawn from the point of reflection. This is because the angle of incidence is equal to the angle of reflection. Also, the opposite sides subtended by these angles in triangles $APQ$ and $RPQ$ have equal lengths. Since $AQ=4cm$, it turns out that $QR$ is also equal to $4cm$.
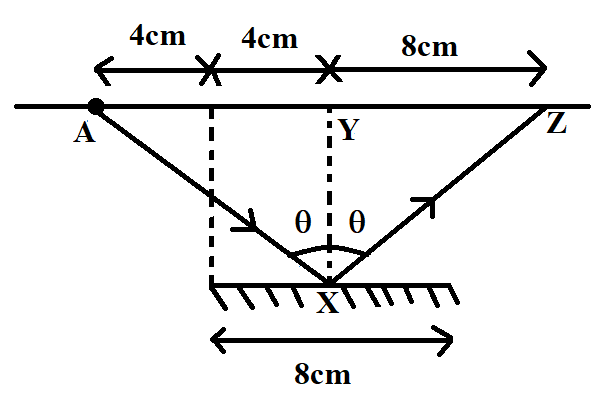
Now, let us take the reflection from point $X$. The incident ray coming from the light source gets reflected and forms a spot on the wall at a distance of $8cm$ from the extended perpendicular tangent, drawn from the point of reflection. This is because the angle of incidence is equal to the angle of reflection. Also, the opposite sides subtended by these angles in triangles $AXY$ and $ZXY$ have equal lengths. Since $AY=8cm$, it turns out that $YZ$ is also equal to $8cm$.
Similarly, let us take the reflection from point $M$. The incident ray coming from the light source gets reflected and forms a spot on the wall at a distance of $12cm$ from the extended perpendicular tangent, drawn from the point of reflection. This is because the angle of incidence is equal to the angle of reflection. Also, the opposite sides subtended by these angles in triangles $AMN$ and $OMN$ have equal lengths. Since $AN=12cm$, it turns out that $NO$ is also equal to $12cm$.
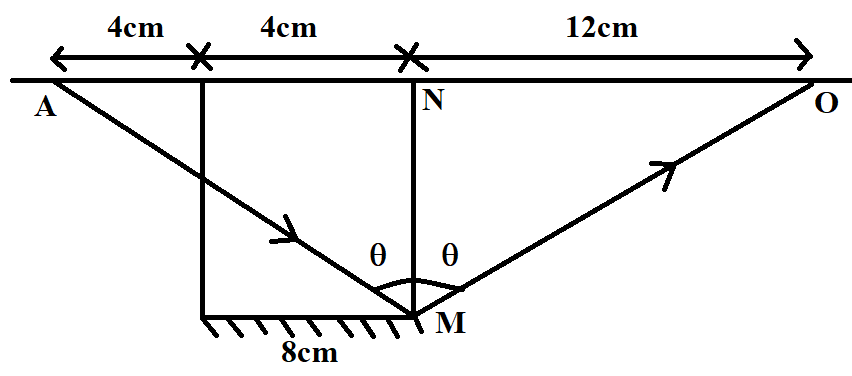
Now, if we combine all these diagrams and observe carefully, we can see that the spot of the light source has a size equal to the length between $Q$ and $O$. Length between $Q$ and $O$ is given by
$QO=24cm-8cm=16cm$
We are given that the size of the spot is equal to $\dfrac{32}{x}cm$.
Equating both the above expressions together, we have
$\dfrac{32cm}{x}=16cm\Rightarrow x=2cm$
Therefore, the value of $x$ is $2$
Note:
While approaching such questions, students need to keep in mind that it is important to draw diagrams. Diagrams can easily figure out distances, as done in the above solution. It is also important to know that the speed of mirror given in the question has nothing to do with the size of the spot, or the value of $x$, in this particular situation. Students need to recognise this at first and avoid further confusions.
Complete answer:
We are given that a plane mirror of length $8cm$ is moving with speed $3m{{s}^{-1}}$ towards a wall in the situation as shown in the following figure.
Clearly, the distance of the light source from the wall is $4cm$. We are required to find the size of the spot, projected on the wall, after reflection from the plane mirror.
According to the laws of reflection, the angle of incidence is equal to the angle of reflection. Angle of incidence is nothing but the angle between the incident ray of light source and the perpendicular tangent drawn at the point of incidence on the plane mirror. Similarly, angle of reflection is nothing but the angle between the reflected ray and the perpendicular tangent drawn at the point of reflection. Clearly, point of incidence is equal to point of reflection.
We also know that if two angles of two different triangles are equal, both these angles will subtend equal lengths on the opposite sides of these triangles.
Now, let us apply the law of reflection and the property of equal angles in triangles to each incident ray and its corresponding reflected ray. We consider three points of reflection-the first one being the extreme left point of the plane mirror, the second one being the midpoint of the plane mirror and the third one being the extreme right point of the plane mirror. Clearly, these points are $P,X$ and $M$, respectively, as can be seen from the figure given above.
Let us take the case of reflection from point $P$. The incident ray coming from the light source gets reflected and forms a spot on the wall at a distance of $4cm$ from the extended perpendicular tangent, drawn from the point of reflection. This is because the angle of incidence is equal to the angle of reflection. Also, the opposite sides subtended by these angles in triangles $APQ$ and $RPQ$ have equal lengths. Since $AQ=4cm$, it turns out that $QR$ is also equal to $4cm$.
Now, let us take the reflection from point $X$. The incident ray coming from the light source gets reflected and forms a spot on the wall at a distance of $8cm$ from the extended perpendicular tangent, drawn from the point of reflection. This is because the angle of incidence is equal to the angle of reflection. Also, the opposite sides subtended by these angles in triangles $AXY$ and $ZXY$ have equal lengths. Since $AY=8cm$, it turns out that $YZ$ is also equal to $8cm$.
Similarly, let us take the reflection from point $M$. The incident ray coming from the light source gets reflected and forms a spot on the wall at a distance of $12cm$ from the extended perpendicular tangent, drawn from the point of reflection. This is because the angle of incidence is equal to the angle of reflection. Also, the opposite sides subtended by these angles in triangles $AMN$ and $OMN$ have equal lengths. Since $AN=12cm$, it turns out that $NO$ is also equal to $12cm$.
Now, if we combine all these diagrams and observe carefully, we can see that the spot of the light source has a size equal to the length between $Q$ and $O$. Length between $Q$ and $O$ is given by
$QO=24cm-8cm=16cm$
We are given that the size of the spot is equal to $\dfrac{32}{x}cm$.
Equating both the above expressions together, we have
$\dfrac{32cm}{x}=16cm\Rightarrow x=2cm$
Therefore, the value of $x$ is $2$
Note:
While approaching such questions, students need to keep in mind that it is important to draw diagrams. Diagrams can easily figure out distances, as done in the above solution. It is also important to know that the speed of mirror given in the question has nothing to do with the size of the spot, or the value of $x$, in this particular situation. Students need to recognise this at first and avoid further confusions.
Recently Updated Pages
Two men on either side of the cliff 90m height observe class 10 maths CBSE
What happens to glucose which enters nephron along class 10 biology CBSE
Cutting of the Chinese melon means A The business and class 10 social science CBSE
Write a dialogue with at least ten utterances between class 10 english CBSE
Show an aquatic food chain using the following organisms class 10 biology CBSE
A circle is inscribed in an equilateral triangle and class 10 maths CBSE
Trending doubts
Which of the following does not have a fundamental class 10 physics CBSE
What is the full form of POSCO class 10 social science CBSE
State BPT theorem and prove it class 10 maths CBSE
A Gulab jamun contains sugar syrup up to about 30 of class 10 maths CBSE
Write the difference between soap and detergent class 10 chemistry CBSE
A triangle ABC is drawn to circumscribe a circle of class 10 maths CBSE