Question

A plane meets the coordinate axes in A, B, and C such that the centroid of the triangle ABC is the point (p, q, r). If the equation of the plane is $\dfrac{x}{p}+\dfrac{y}{q}+\dfrac{z}{r}=k$, then find the value of k?

Answer 1

Hint: First of all, we are going to find the coordinates of points A, B, and C. Coordinates of A is found by putting y and z as 0 in the equation of a plane, coordinates of B is found by putting x and z as 0 and coordinates of C is found by putting x and y as 0. Now, we know that if we have three coordinates of triangle ABC then the coordinates of the centroid is calculated by adding all the x coordinates of vertices A, B and C and then dividing this addition by 3. Similarly, y – coordinates of the centroid are found by adding all the y – coordinates of A, B, and C vertices and then divide this addition by 3. Similarly, find the coordinates for z in the centroid. And then equate the x, y, and z coordinates of the centroid by p, q, and r respectively. From these three equations, you will get the value of k.

Complete step by step answer:
In the above problem, we have given the following equation of a plane:
$\dfrac{x}{p}+\dfrac{y}{q}+\dfrac{z}{r}=k$
Now, we are going to find the coordinates of A, B and C.
The coordinates of A is calculated by putting y and z as 0 in the given equation of plane and we get,
$\begin{align}
  & \Rightarrow \dfrac{x}{p}+\dfrac{0}{q}+\dfrac{0}{r}=k \\
 & \Rightarrow \dfrac{x}{p}=k \\
 & \Rightarrow x=kp \\
\end{align}$
So, the coordinates of A are $\left( kp,0,0 \right)$.
The coordinates of B is calculated by putting x and z as 0 in the given equation of plane and we get,
$\begin{align}
  & \Rightarrow \dfrac{0}{p}+\dfrac{y}{q}+\dfrac{0}{r}=k \\
 & \Rightarrow \dfrac{y}{q}=k \\
 & \Rightarrow y=kq \\
\end{align}$
So, the coordinates of B is equal to $\left( 0,kq,0 \right)$.
The coordinates of C is calculated by putting y and x as 0 in the given equation of plane and we get,
$\begin{align}
  & \Rightarrow \dfrac{0}{p}+\dfrac{0}{q}+\dfrac{z}{r}=k \\
 & \Rightarrow \dfrac{z}{r}=k \\
 & \Rightarrow z=kr \\
\end{align}$
So, the coordinates of C is equal to $\left( 0,0,kr \right)$.
Now, we know that if we have three vertices of a triangle ABC then the formula for the centroid of the triangle is as follows:

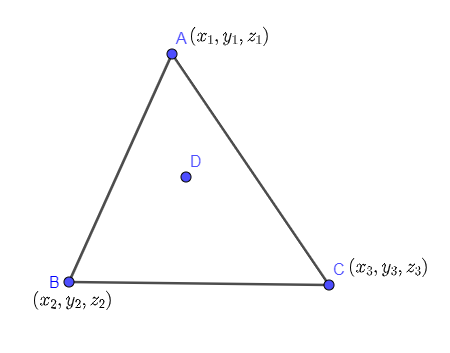
The coordinates of the centroid D is equal to:
$D\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3},\dfrac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3} \right)$
Now, finding the centroid for given vertices A, B and C by using the above relation we get,
$D\left( \dfrac{kp+0+0}{3},\dfrac{0+kq+0}{3},\dfrac{0+0+kr}{3} \right)$
It is given that the coordinates of triangle ABC is (p, q, r) so equating each of the coordinates to the above coordinates we get,
$\begin{align}
  & \dfrac{kp}{3}=p \\
 & \Rightarrow k=3; \\
 & \dfrac{kq}{3}=q \\
 & \Rightarrow k=3; \\
 & \dfrac{kr}{3}=r \\
 & \Rightarrow k=3; \\
\end{align}$
Hence, we have found the value of k as 3.

Note: To solve the above problem, we need to know the formula for finding the centroid of triangle ABC. Also, we should know when a plane cuts the x, y, and z-axis then how we can find the coordinates of the points where the plane cuts the coordinate axes.