Question

A plane is inclined at an angle θ with horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then find the minimum force that has to be applied on the body to make the body just move up the inclined plane.
A. $mg\sin \theta $
B. $\mu mg\cos \theta $
C. $\mu mg\cos \theta -mg\sin \theta $
D. $\mu mg\cos \theta +mg\sin \theta $

Answer 1

Hint: when a plane is inclined at some angle θ with respect to the horizontal, then the no. of forces should be acted on the body. There is force of friction and the weight of the object which acts in downward direction has its two components, one is in the direction opposite to the force of friction and another should be in the direction opposite to the normal reaction.

Complete answer:
A body of mass m resting on the inclined plane at an angle θ with horizontal, having coefficient of friction μ, is represented by the figure shown below. The angle of friction is also called the angle of repose.
Also there are two forces acting on the body placed at the inclined surface are: force due to gravity and normal force that acts in perpendicular to the body.

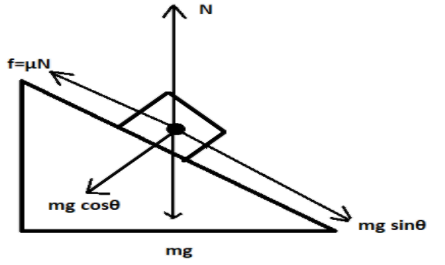
Frictional force is the force that should be applied to prevent the body from falling. The coefficient of friction is the ratio of force of friction and normal force.
$\mu =f/N$
The mass m of the body acts in downward direction due to the effect of gravity. Then the parallel-component of the weight acts in the opposite direction to the force of friction. The perpendicular-component of weight acts in the opposite direction to the normal force N which balances each other.
Also the acceleration due to gravity is along the parallel component.
The minimum force applied to the body to move up is the subtraction of force of friction acting in upward direction and the x-component of weight.
Negative sign is used because the parallel component of weight (mg sinѲ) acts in downward direction.
Therefore, the minimum force that should be applied to make the body up the inclined plane is given as:
$\begin{align}
  & F=f-mg\sin \theta \\
 & F=\mu N-mg\sin \theta \\
\end{align}$
Also n is the normal force which is balanced by perpendicular component of weight, it can be written as:
$N=\mu mg\cos \theta $
Hence, the minimum force applied is given by:
$\begin{align}
  & F=\mu N-mg\sin \theta \\
 & F=\mu mg\cos \theta -mg\sin \theta \\
\end{align}$

So, option C is the correct answer.

Note:
A body is placed on the inclined plane at angle θ with horizontal, the weight of the body acts downward to the plane. It has two components along x and y axes. The normal force is counterbalanced with the y- component of weight, and the force of friction acts in upward direction. The minimum force applied to move up the body is force of friction minus the x- component of weight.