Question

A plane is inclined at an angle $\alpha ={{30}^{\circ }}$ with respect to the horizontal. A particle is projected with a speed of $u=2m{{s}^{-1}}$ from the base of the plane, making an angle $\theta ={{15}^{\circ }}$ with respect to the plane as shown in the figure. The distance from the base at which the particle hits the plane is close to:

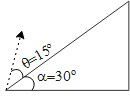
a)14cm
b) 20cm
c) 18cm
d)26cm

Answer 1

Hint: In the above question we are asked to determine the distance from the base of the plane to the point on the plane where the given particle hits it. In other words we have to determine the range along the plane. First we need to consider the plane as our x-axis and accordingly resolve the initial components of velocity and acceleration due to gravity (g). Further we will consider the equation of the plane of the particle along the plane and accordingly determine the range along the plane.

Formula used:
$R={{u}_{X}}t+\dfrac{1}{2}{{g}_{X}}{{t}^{2}}$
$t=\dfrac{2{{u}_{Y}}}{{{g}_{Y}}}$

Complete step-by-step answer:

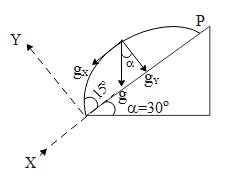
In the above diagram we have resolved for g and using the same diagram we can resolve the initial and final velocity along the plane. In the above diagram we can see that the particle hits the plane at point P. If U is the initial velocity of the particle, than the initial component of velocity along the X-axis in the above figure is equal to ${{u}_{X}}=UCos\theta $ and along y-axis it is equal to ${{u}_{Y}}=USin\theta $ the acceleration due to gravity always acts downwards. Hence if we consider the above figure the horizontal component of g i.e. ${{g}_{X}}=gSin\alpha $ and vertical component ${{g}_{Y}}=gCos\alpha $ are in opposite direction as per the direction of the axes is concerned. The time ‘t’ of flight i.e. from the base of the plane to the point P is given by,
$t=\dfrac{2{{u}_{X}}}{{{g}_{Y}}}$
Substituting the required quantities in the above equation we get,
$\begin{align}
  & t=\dfrac{2{{u}_{Y}}}{{{g}_{Y}}}\text{, }\because {{u}_{Y}}=USin\theta \text{ }and\text{ }{{g}_{Y}}=gCos\alpha \\
 & t=\dfrac{2USin\theta }{gCos\alpha }\text{, }\because \theta ={{15}^{\circ }}\text{ }and\text{ }\alpha ={{30}^{\circ }} \\
 & \Rightarrow t=\dfrac{2\times 2m{{s}^{-1}}Sin{{15}^{\circ }}}{10m{{s}^{-2}}Cos{{30}^{\circ }}}=\dfrac{4\times 0.258}{10\times 0.866} \\
 & \Rightarrow t=0.119\sec s \\
\end{align}$
The distance(R) from the base of the plane to the point P is given by,
$R={{u}_{X}}t+\dfrac{1}{2}{{g}_{X}}{{t}^{2}}$
Therefore substituting the required quantities in the above equation we get R as,
$\begin{align}
  & R={{u}_{X}}t+\dfrac{1}{2}{{g}_{X}}{{t}^{2}}\text{, }\because {{u}_{X}}=UCos\theta \text{ }and\text{ }{{g}_{X}}=gSin\alpha \\
 & \Rightarrow R=UCos\theta t+\dfrac{1}{2}gSin\alpha {{t}^{2}}\text{, }\because UCos\theta =1.931\text{ }and\text{ }gSin\alpha =5 \\
 & \Rightarrow R=1.931t+\dfrac{1}{2}5{{t}^{2}}\text{, }\because t=0.119 \\
 & \Rightarrow R=1.931\times 0.119+\dfrac{1}{2}5\times {{(0.119)}^{2}} \\
 & \Rightarrow R=0.264m\simeq 26cm \\
\end{align}$
Hence the correct answer of the above question is option d.

So, the correct answer is “Option d”.

Note: The above question can also be solved by obtaining the equations of the trajectory of the particle and the plane i.e. just basically a line. What we have to do is that we have to obtain the point of intersection of the two. Further accordingly using Pythagoras theorem we can determine R. But his method will involve a lot of mathematics.