Question

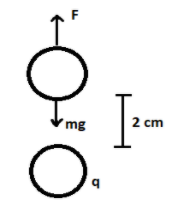
A pith ball of mass $9 \times {10^{ - 5}}kg$ carries a charge of $5\mu C$.What must be charge in another pith ball placed directly 2 cm above given pith ball such that they are held in equilibrium?
A) $3.2 \times {10^{ - 11}}C$
B) $7.84 \times {10^{ - 12}}C$
C) $1.2 \times {10^{ - 13}}C$
D) $1.6 \times {10^{ - 19}}C$

Answer 1

Hint: A pith ball is to be placed on another pith ball, it will be held in equilibrium when the opposite forces will be equal i.e. when force of attraction between the charges will be equal to the weight of the pith ball.

Formula used:
$F = K\dfrac{{{q_1}{q_2}}}{{{r^2}}}$ where q denotes the magnitude of respective charges and r, the distance between them.
$K = \dfrac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}N{m^2}/{C^2}$
value of acceleration due to gravity g is $9.8m/{s^2}$

Complete step by step answer:
If we have to place another pith ball 2 cm above the first one, then its weight should be balanced and equal to the force of attraction existing between the two pith balls of varying charges.
${F_{attr}} = mg$
According to Coulomb’s law, the force of attraction between two charges is directly proportional to the product of the magnitude of their charges and inversely proportional to the square of the distance between them.

$F \propto \dfrac{{{q_1}{q_2}}}{{{r^2}}}$
Here, $K = \dfrac{1}{{4\pi {\varepsilon _0}}}$ is used as the proportionality constant.
$ \Rightarrow \dfrac{1}{{4\pi {\varepsilon _0}}} \times \dfrac{{{q_1}{q_2}}}{{{r^2}}} = mg$
Here,
Charge on the first body \[\left( {{q_1}} \right)\] = $5\mu C$ or $5 \times {10^{ - 6}}C$ $\left( {\because 1C = {{10}^6}\mu C} \right)$
Charge on the second body \[\left( {{q_2}} \right)\] = q (let)
Distance between the two charges (r) = 2 cm or $2 \times {10^{ - 2}}m$ $\left( {\because 1m = 100cm} \right)$
Given mass of the ball (m) = $9 \times {10^{ - 5}}kg$
Value of acceleration due to gravity (g) = $9.8m/{s^2}$
Value of K: $\dfrac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}N{m^2}/{C^2}$
Substituting the values, we get:
$
\dfrac{{9 \times {{10}^9} \times 5 \times {{10}^{ - 6}} \times q}}{{{{(2 \times {{10}^{ - 2}})}^2}}} = 9 \times {10^{ - 5}} \times 9.8 \\
\Rightarrow q = \dfrac{{9 \times {{10}^{ - 5}} \times 9.8 \times {{(2 \times {{10}^{ - 2}})}^2}}}{{9 \times {{10}^9} \times 5 \times {{10}^{ - 6}}}} \\
\Rightarrow q = \dfrac{{9 \times {{10}^{ - 5}} \times 9.8 \times 4 \times {{10}^{ - 4}} \times {{10}^6} \times {{10}^{ - 9}}}}{{9 \times 5}} \\
 \Rightarrow q = 7.84 \times {10^{ - 12}}C \\
 $

Therefore, the charge in another pith ball placed directly 2 cm above a given pith ball such that they are held in equilibrium should be $7.84 \times {10^{ - 12}}C$.

Note:
When we use the word equilibrium, it means that the forces acting on the body are balanced, the forces acting in opposite directions should be equal.
While solving the powers, keep in mind that when the base number is same (10 in the above case), their powers are added in case of multiplication and subtracted in case of division and when we take any number from numerator to denominator or vice-versa, the sign of the power changes.