Question

A piece of wire is bent in the shape of a parabola $y=kx^{2}$ y-axis vertical with a bread of mass $m$ on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration$a$. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
\[\begin{align}
  & A.\dfrac{a}{gk} \\
 & B.\dfrac{a}{2gk} \\
 & C.\dfrac{2a}{gk} \\
 & D.\dfrac{a}{4gk} \\
\end{align}\]

Answer 1

Hint: The bead on the parabola will have a normal. When the normal is resolved, we will see that it is equal to the acceleration of the bead and the force due to gravitation. We can equate the respective component to the acceleration, to find the new equilibrium position of the bead.

Formula:
$tan \theta=\dfrac{a}{g}$ and $tan\theta=\dfrac{dy}{dx}$

Complete answer:
Let the position of the bead of mass $m$ on the parabola at any instant be $x$. Given that the equation of parabola $y=kx^{2}$
Let the parabola be accelerated with a constant acceleration $a$ along the negative x-axis.
Clearly, the parabola will experience a normal force denoted as $N$, a force due to acceleration of the parabola $F=ma$ and the force due to gravitation be $F_{g}=mg$, as shown in the figure.

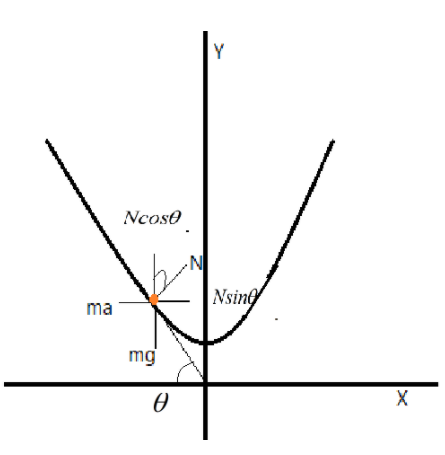
Then we can resolve the normal into two components, $Nsin\theta $ and $Ncos\theta$.
Clearly, $Nsin\theta=ma$ and $Ncos\theta=mg$.
Taking the ratio , $\dfrac{Nsin\theta}{Ncos\theta}=\dfrac{ma}{mg}$
Then we get $tan \theta=\dfrac{a}{g}$
Also from mathematics, we know that $tan\theta=\dfrac{dy}{dx}$
And differentiating $y=kx^{2}$, we get $\dfrac{dy}{dx}=2kx$
Or$tan\theta=2kx$
For the bead to be in equilibrium, it must satisfy the condition $2kx=\dfrac{a}{g}$
Or,$x=\dfrac{a}{2kg}$
Hence the new equilibrium position of the bead is $x=\dfrac{a}{2kg}$

Hence the answer is \[B.\dfrac{a}{2gk}\]

Note:
Here we are using mathematical differentiation of the parabolic equation to find the position of the bead. Also notice that the differentiation of an equation is nothing but the slope of the equation with the x axis. Here we are accelerating the parabola along the negative x- axis, hence we get $Nsin\theta=ma$. If the parabola is accelerated along the positive x-axis, we will get $Nsin\theta=-ma$. As both the $Nsin\theta$ and $F_{g}=mg$ act in the same direction and their sum is equal to $0$ for the bead to obtain equilibrium.