Question

A piece of iron of density 7800$kg{{m}^{-3}}$ and volume 100$c{{m}^{3}}$ is completely immersed in water, calculate apparent weight of iron piece in water.
[Take , $g=10m{{s}^{-2}}$]
A. 6.8N
B. 1N
C. 7.8N
D. 8.8 N

Answer 1

Hint: When a body is immersed in a liquid, the liquid exerts a force of buoyancy on the body in the upward direction. Find the buoyancy force and the gravitational force on the iron piece by using the formulas ${{F}_{g}}=mg$ and ${{F}_{B}}=\rho {{V}_{s}}g$. Calculate the mass of the body by $Density=\dfrac{mass}{volume}$. The apparent weight of the body will be ${{F}_{g}}-{{F}_{B}}$.
Formula used:
${{F}_{g}}=mg$
${{F}_{B}}=\rho {{V}_{s}}g$
$Density=\dfrac{mass}{volume}$

Complete step by step answer:
We know that earth exerts a force called gravitational force (${{F}_{g}}$) on a body within its gravity. The nature of this force is always attractive. Therefore, it is always directed downwards (i.e. is towards the centre of earth).
If the mass of the body is m, then the force gravity is equal to ${{F}_{g}}=mg$, where g is the acceleration of the body due to gravity.
When a body is put in water or any other liquid, the liquid exerts a force on the substance. This force is called upthrust or buoyancy force (${{F}_{B}}$). The direction of this force is always in the upward direction i.e. in the opposite direction of the gravitational force. The free body diagram of a body in water is shown in the figure below.

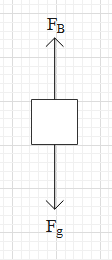
The value of buoyancy force is given as ${{F}_{B}}=\rho {{V}_{s}}g$.
Here, $\rho $ is the density of the liquid in which the body is immersed, V is the volume of the body that is submerged in the liquid.
Therefore, the net force on the body is ${{F}_{net}}={{F}_{g}}-{{F}_{B}}$.
If we place the body on a massless weighing machine, the weighing machine will measure the weight of the body equal to ${{F}_{net}}$ and this is less than mg. Therefore, we call it the apparent weight of the body.
Let us calculate the gravitational force on the piece of iron. For that let us first calculate its mass (m).
We will use the formula for density, i.e. $Density=\dfrac{mass}{volume}$.
$\Rightarrow mass=density\times volume$
Here, the density of the body is given as 7800$kg{{m}^{-3}}$ and its volume is 100$c{{m}^{3}}=100\times {{10}^{-6}}{{m}^{3}}={{10}^{-4}}{{m}^{3}}$
Hence,
$\Rightarrow m=7800\times {{10}^{-4}}kg$
This means that ${{F}_{g}}=mg=7800\times {{10}^{-4}}\times 10=7.8N$
Let us calculate the buoyancy force on the body. Here, it is said that the iron piece is immersed completely. This means V=${{10}^{-4}}{{m}^{3}}$.
The density of water is ${{10}^{3}}kg{{m}^{-3}}$. Hence, $\rho ={{10}^{3}}kg{{m}^{-3}}$.
Therefore,
${{F}_{B}}=\rho {{V}_{s}}g={{10}^{3}}\times {{10}^{-4}}\times 10=1N$.
Therefore,
Apparent weight = ${{F}_{net}}={{F}_{g}}-{{F}_{B}}=7.8-1=6.8N$.
Hence, the correct option is A.
Note: Note that buoyant force is a variable force. It depends on the volume of the body submerged under the liquid. The maximum buoyant force is equal to ${{F}_{B}}=\rho Vg$, where V is the complete volume of the body.
If the gravitational force is less than or equal to the maximum buoyant force, then the body will float.
If the gravitational force is more than the maximum buoyant force, then the body will sink in the liquid.