Question

A piece of aluminum with mass $1.00kg$ and density $2700kg/{m^3}$ is suspended in air from a string and then completely immersed in a container of water. Calculate the tension in the string (a) before and (b) after the metal is immersed. Take ${\text{g = 10m/}}{{\text{s}}^2}$, density of water $ = {10^3}{\text{ kg}}{{\text{m}}^{ - 3}}$.
A. 0N, 2.3N
B. 2.3N, 10N
C. 5N, 1.15N
D. None of these

Answer 1

Hint: When the aluminum piece is suspended in air, Tension carried will be given by T = mg. And when the aluminum piece is immersed in water, based on the density of liquid, along with Tension T, there will be buoyant force acting on the aluminum piece. So to calculate the tension in the string we need to use the buoyant force as well.

Complete step-by-step answer:
Given, mass of place of aluminum, m $ = 1{\text{ kg}}$
Density of aluminum, ${\rho _{\text{s}}} = 2700{\text{ kg/}}{{\text{m}}^3}$
Density of water, ${\rho _{\text{w}}} = 1000{\text{ kg/}}{{\text{m}}^3}$

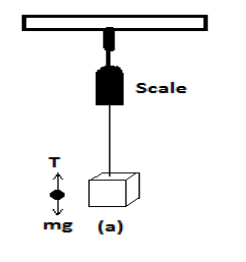
As shown in figure, we have to find tension in the string in each case.

a. When the aluminum piece is suspended in air
Tension, T= mg based on the figure above
Tension force is defined as the force that is transmitted through a rope, string or wire when pulled by force acting from opposite sides. The tension force is directed over the length of the wire and pulls energy equally on the bodies at the ends.

Therefore, T$ = 1 \times 10 = 10{\text{N}}$

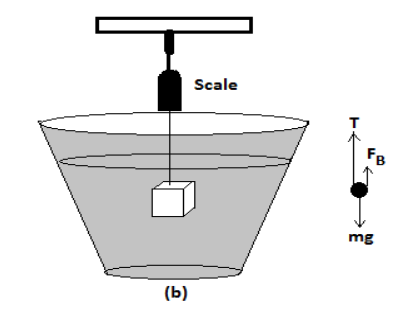
b. When the aluminum piece is completely immersed in water,
${\text{mg = T + }}{{\text{F}}_B}$ (From figure)
Where, ${{\text{F}}_{\text{B}}}$= buoyant force acting on aluminum
The buoyant force comes from the pressure exerted on the object by the fluid. Because the pressure increases as the depth increases, the pressure on the bottom of an object is always larger than the force on the top – hence the net upward force

${\text{T = }}$Tension in the string
\[\therefore {\rm T}{\text{ = mg - }}{{\text{F}}_{\text{B}}}\]
\[{\text{T}} = {\rho _{\text{s}}}{{\text{V}}_{\text{s}}}{\text{g}} - {\rho _{\text{L}}}{{\text{V}}_{\text{L}}}{\text{g}}\]
\[ = \left( {{\rho _{\text{s}}}{{\text{V}}_{\text{s}}} - {\rho _{\text{L}}}{{\text{V}}_{\text{S}}}} \right){\text{g}}\]
\[ = {\rho _{\text{s}}}{{\text{V}}_{\text{s}}}\left( {1 - \dfrac{{{\rho _{\text{L}}}}}{{{\rho _{\text{s}}}}}} \right){\text{g}}\]
\[ = \left( {{\rho _{\text{s}}}{{\text{V}}_{\text{s}}}{\text{g}}} \right)\left( {1 - \dfrac{{{\rho _{\text{L}}}}}{{{\rho _{\text{s}}}}}} \right)\]
\[ = \left( {{\text{mg}}} \right)\left( {1 - \dfrac{{{\rho _{\text{L}}}}}{{{\rho _{\text{s}}}}}} \right)\]
Or ${{\text{T}}^\prime } = 1 \times 10\left( {1 - \dfrac{{1000}}{{2700}}} \right)$
$ \Rightarrow {{\text{T}}^\prime } = 10\left( {1 - \dfrac{{10}}{{27}}} \right)$
$ \Rightarrow {{\text{T}}^\prime } = 10\left( {\dfrac{{27 - 10}}{{27}}} \right)$
$ \Rightarrow {{\text{T}}^\prime } = 10\left( {\dfrac{{17}}{{27}}} \right) = 6.296{\text{ N}}$
Hence, the tension in the string before and after the metal is immersed are 10N and 6.296N respectively.

Note: SI unit for force is newton and CGS unit of force is dyne. We need to know the conversions $1{\text{ N}} = 1{\text{ kg}}{\text{. m/}}{{\text{s}}^2}$ and $1{\text{ dyne = 1}}{{\text{0}}^{ - 5}}{\text{N}}$. Buoyancy is the force that causes objects to float. There are three types of buoyancy which are positive, negative and neutral.