Question

A picture is $50cm$ long and $30cm$ broad. What is the area of glass required to cover the picture in one frame?

Answer 1

Hint: In this question, we are given the dimensions of a picture and we are required to find the area of the picture. So, we express area in terms of length of one dimension and from an equation. Then, we find the area of the rectangle using the formula \[A = L \times B\], where L and B are the length and breadth of the rectangle.

Complete step by step solution:
A rectangle is a two dimensional shape with all four angles equal to ${90^ \circ }$ and opposite sides as equal. To determine the area of a rectangle, we have the standard formula $A = L \times B$ where L and B denote the length and breadth of the rectangle. The unit for the area is square units.
So, we are provided with the dimensions of the rectangle.
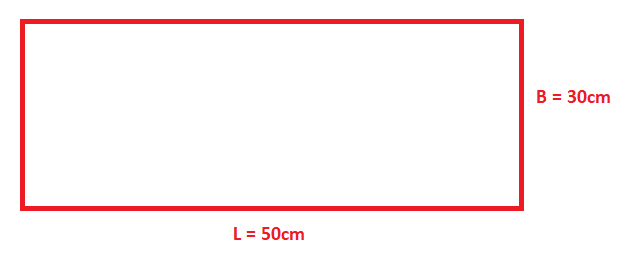
The length of the rectangular picture is given as $50cm$.
The breadth of the picture is given as $30cm$.
Now, we know that the formula for the area of the rectangle with length as L and breadth as B is \[A = L \times B\].

We substitute the values of L and B into the formula to find the area of the picture.
So, we get,
\[ \Rightarrow A = \left( {50cm} \right) \times \left( {30cm} \right)\]
Now, we simplify the calculations and find the product. So, we get,
\[ \Rightarrow A = 1500\,c{m^2}\]
Therefore, the area of the picture is \[1500\,c{m^2}\].
The glass with which the picture is to be covered should be of the same size as the picture itself.
Therefore, the area of the glass required to cover the picture is \[1500\,c{m^2}\].

Note:
Generally the area is the region occupied by the thing. The area of a rectangle is defined as the region occupied by the quadrilateral region. We must know the formulae for area and perimeter of basic shapes like square, rectangle, parallelogram, circle, etc. We also must take care of the calculations while doing such questions. One must have a strong grip over concepts of transposition in order to solve the equation formed in the problem.