Question

What should a piano tuner do to correct the sound of a string that is flat, that is, it plays at a lower pitch that it should?
A. Tighten the string to make the fundamental frequency higher
B. Tighten the string to make the fundamental frequency lower
C. Loosen the string to make the fundamental frequency higher
D. Loosen the string to make the fundamental frequency lower
E. Find a harmonic closer to the desired pitch

Answer 1

Hint: The natural frequency or fundamental frequency, is defined as the lowest frequency of a periodic waveform. In the music field, the fundamental frequency is defined as the musical pitch of the note.
So, we see that the pitch of the music is dependent on the frequency of the sound. So, by varying the pitch to correct the flatness, it is necessary to adjust the tension of the string, which can help solve the issue that the piano tuner is facing in this problem.

Complete step-by-step answer:
Even though a lion’s roar is tremendously ferocious as compared to the buzzing of a tiny bee, you will be surprised to know that the pitch of the buzzing of the bee is very high compared to that of the lion’s roar. This occurs due to a property of the sound known as the pitch, which is dependent on the frequency of the vibration.
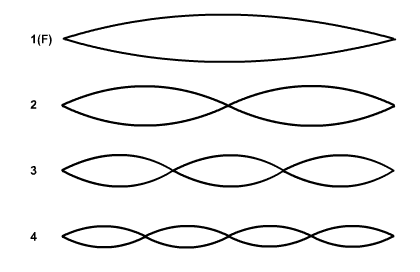
Consider the string of the length L of the piano as shown:

Here, the piano string is vibrating at its fundamental frequency.
Fundamental frequency, ${f_1} = \dfrac{v}{{2L}}$
The wave velocity, $v = \sqrt {\dfrac{T}{m}} $
where T = tension and m = mass per unit length of the string. $m = \dfrac{M}{L}$ where M is mass of the string.
Substituting the wave velocity in the frequency expression, we get –
${f_1} = \dfrac{v}{{2L}}$
${f_1} = \dfrac{{\sqrt {\dfrac{T}{m}} }}{{2L}}$
$ \Rightarrow {f_1} = \dfrac{{\sqrt T }}{{2L\sqrt m }}$
Here, we see that the fundamental frequency, $f \propto \sqrt T $
Thus, if we increase the tension in the string, we can increase the fundamental frequency of the string.

Hence, the correct option is Option A.

Note: The fundamental frequency is the first member of a group of frequencies that the string can acquire, known as the harmonic series. In the harmonic series, the subsequent frequencies of the harmonic series are equal to the positive integral multiples of the fundamental frequency.