Question

A photon of wavelength $\lambda $ is scattered from an electron, which is at rest.The wavelength shift $\Delta \lambda $ is three times of $\lambda $ and the angle of scattering $\theta $ is ${60^o}$. The angle at which the electron recoiled is $\phi $ . The value of $\tan \phi $ is : (electron speed is much smaller than the speed of light)
A. \[0.28\]
B. $0.22$
C. $0.25$
D. $0.16$

Answer 1

Hint: This is an example of matter and radiation interaction; and questions of this type can solve using the conservation of linear momentum. According to this principle, momentum of an isolated system remains constant as long as no external force is applied. Here, this photon and electron system can be considered an isolated system.

Formula used:
-De Broglie wavelength, $\lambda $ , associated with incident photon $ = \dfrac{h}{{p(photon)}}$
Where, $p$ represents momentum and $h$ is planck's constant.
-Initial momentum $(\sum {p_i)} $ $ = $ Final momentum $(\sum {p_f)} $


Complete step by step answer:
We will first find initial and final momentum for both photon and electron and then will apply the conservation of linear momentum.
Initial momentum of photon $ = \dfrac{h}{{\lambda i}}$
Final momentum of scattered photon $ = \dfrac{h}{{\lambda f}}$
Initial momentum of electron $ = 0$
Final momentum of scattered electron $ = p$

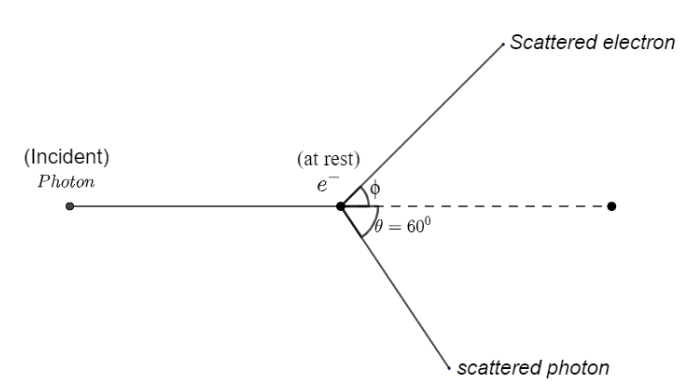
Now, we will first use conservation of linear momentum along x-axis:
$\dfrac{h}{{\lambda_i}} + 0 = \dfrac{h}{{\lambda_f}}\cos \theta + p\cos \phi $.........(1)
Then along the y-axis:
$0 = \dfrac{h}{{\lambda_f}}\sin \theta - p\sin \phi$................(2)
Now use the given values:
$\theta = {60^o}$ ;
$\Rightarrow \lambda_i = \lambda $ ;
\[\Rightarrow \Delta \lambda = 3\lambda_i = 3\lambda \\
\Rightarrow \lambda_f - \lambda_i = 3\lambda \;\; \\ \]
$\Rightarrow \lambda_f = 4\lambda$...................(3)
After using these values, equation $(1)$ becomes-
$p\cos \phi = \dfrac{{7h}}{{8\lambda }}$...............(4)
And equation $(2)$ becomes-
$p\sin \phi = \dfrac{{\sqrt 3 h}}{{8\lambda}}$...........(5)
After dividing equation $(4)$ and $(5)$ , we get –
$\therefore \tan \phi = \dfrac{{\sqrt[{}]{3}}}{7} = 0.247$ ; which is the required value.

Hence, the correct answer is option C.

Note: This phenomenon of wavelength shift of radiation on interaction with matter is called Compton Effect. It was discovered by A.H. Compton in 1923. This effect provides direct evidence of the particle nature of radiation. The wavelength shift is independent of incident beam and the type of material used for scattering; it only depends on the scattering angle. The method of conservation of linear momentum used here is very general and comes handy in solving many questions, so students are advised to practice this method.