Question

A person walks $25{}^\circ $ north of east for 3.18km. How far would she have to walk due north and then due east to arrive at the starting point?
A. toward north 2.88km and towards east 1.34km
B. toward north 2.11km and towards east 2.11km
C. toward north 1.25km and towards east 1.93km
D. toward north 1.34km and towards east 2.88km

Answer 1

Hint: There are four core directions east, west, north, and south. When a person moves $25{}^\circ $ north of east it refers that the path covered by the person is at an inclination of $25{}^\circ $ from the east towards the north. The Law of alternating angle states that the alternating angle formed by the interaction of two parallels with the transversal is always the same.

Complete answer:
According to the question given in the question. The girl performs a displacement of 3.18km in $25{}^\circ $ the north of the east. The condition can be understood with more clarity by the diagram shown below.

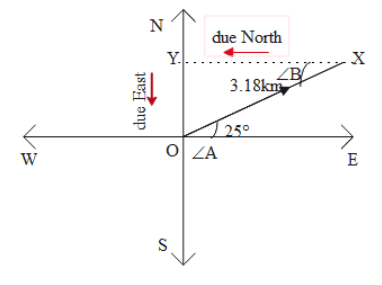
When she takes a move towards due north (west) while initializing her journey to reach the starting point, the angle by which she will change her path will be \[25{}^\circ \] towards the north.
Mathematically:
$\angle A=\angle B=25{}^\circ $
A triangle OXY is formed while returning to the original point, such that:
The path moved by 3.18km is represented as the hypotenuse $(H)$.
Movement due north forms the base $(B)$ of the triangle.
Movement due east represents the perpendicular side $(P)$ of the triangle.
By applying trigonometric ratios on triangle OXY (refer to the above diagram):
$\begin{align}
  & \sin (25{}^\circ )=\dfrac{P}{H}=\dfrac{P}{3.18} \\
 & \cos (25{}^\circ )=\dfrac{B}{H}=\dfrac{B}{3.18} \\
\end{align}$
So the path covered due North will be:
$\begin{align}
  & B=H(\cos (25{}^\circ )) \\
 & B=3.18(0.90630) \\
 & B=2.88km \\
\end{align}$
After reaching a point after moving a distance of 2.88km due north. She has to move towards due east to reach the starting point.
So, the path cover due east to reach the starting point will be:
$\begin{align}
  & P=H(\sin (25{}^\circ )) \\
 & P=3.18(0.42261) \\
 & P=1.34km \\
\end{align}$
So the path covered due north and due east to reach the initial point are 2.88km and 1.34km respectively.

So the correct option which represents these values is Option A.

Note:
When a person covers a certain distance by following the shortest path is known displacement. If a person is walking in a loop and reaches its initial point from where he stated, then the total displacement is said to be zero. The work done by the person moving in a closed path is said to be zero as there is no displacement.