Question

A person walks $25.0^{\circ}$ north of east for $3.10\;km$. How far due north and how far due east would she have to walk to arrive at the same location?

Answer 1

Hint: Begin by charting out a diagram with the necessary cardinal directions. Carefully trace the path the person takes in both cases keeping in mind the distance she travels as well as the direction in which she moves with respect to the horizontal and vertical axes. Once you’ve done this, you should be able to see that this problem can be trigonometrically solved since your map virtually entails a triangle.
Using the appropriate sine and cosine relations with respect to the perpendicular, base and hypotenuse of the triangle, arrive at the required distances she’d need to walk due north and due east.

Complete Step-by-Step Solution:
Let us deconstruct the problem and chart out what’s given to us. We are given that a person walks $3.10\;km$ from O, in a direction $25^{\circ}$ North of East, to reach a point P. This is given as the path $OP=3.10\;km$ in the following diagram, with $\angle POB = 25^\circ$

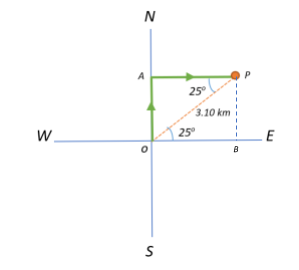
Now, if she was about to reach the point P by first walking due north from O and then due east, we are required to find the distance (OA and AP) she would have to travel in the respective directions.

From the figure, we see that $\angle OPA$ and $\angle POB$ are interior alternate angles.
$\Rightarrow \angle OPA=\angle POB = 25^{\circ}$

This is because:
 $\angle POB = 25^{\circ} \Rightarrow \angle AOP = 90-25=65^{\circ} \Rightarrow \angle OPA = 180-(\angle OAP + \angle AOP) = 180-(90+65)=25^{\circ}$, since sum of all interior angles in a triangle is $180^{\circ}$

Now, we consider $\triangle OAP$ with $\angle OPA = 25^{\circ}$.
$\Rightarrow sin\;25^{\circ} = \dfrac{OA}{OP} \Rightarrow OA = OP \times sin\;25^{\circ} = 3.10 \times 0.42 \Rightarrow OA= 1.31\;km$

Similarly, $cos\;25^{\circ} = \dfrac{AP}{OP} \Rightarrow AP = OP \times cos\;25^{\circ} = 3.10 \times 0.91 \Rightarrow AP = 2.81\;km$

Therefore, the person would have to travel $1.31\;km$ due North and $2.81\;km$ due East to arrive at the same location P.

Note:
An alternate way to solve this would be to treat the distance she initially travels as a displacement vector and resolve it into its horizontal and vertical components to get the component of this vector in the east and north directions respectively.

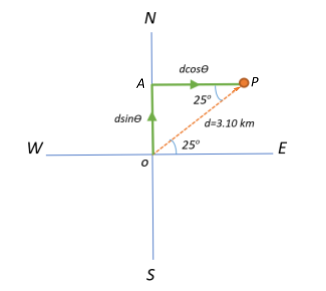
The horizontal component would be $AP =3.10\;cos25^{\circ}$ and the vertical component would be $OA = 3.10\;sin25^{\circ}$ which are similar to $cos25^{\circ}= \dfrac{AP}{OP}$ and $sin25^{\circ} = \dfrac{OA}{OP}$ which is what we got subsequently anyways.